Краткие сведения из теории. Линза – это один из основных элементов оптических систем, предназначенных для получения оптических изображений

Линза – это один из основных элементов оптических систем, предназначенных для получения оптических изображений. Она представляет собой оптически прозрачное тело, ограниченное с двух сторон сферическими поверхностями. Если расстояние О₁О₂ (рис. 1) между этими поверхностями значительно меньше радиусов кривизны, то линза называется тонкой. Ее вершины О₁ и О₂ в этом случае можно считать совпадающими в точке О, называемой оптическим центром линзы. Причем ось, проходящая через оптический центр линзы и центры кривизны ее преломляющих поверхностей, называется главной оптической осью линзы (прямая РР¢, рис. 1).

Рис 1

Если направить луч света параллельно главной оптической оси, то преломившись, он пройдет через точки F₁ или F₂ (в зависимости от того, лежащие на главной оптической оси линзы. Эти точки называют главными фокусами линзы, а сама линза, преломляющая лучи таким образом, называется собирающей (рис. 1, а). Если же после преломления светового луча линзой через точки F₁ или F₂ (главные фокусы) можно провести лишь прямую, представляющую продолжение преломленного луча в направлении, обратном направлению его распространения, то такая линза называется рассеивающей (рис. 1, б).

Расстояние между оптическим центром линзы и ее главными фокусами (расстояния f₁ или f₂) называют главными фокусными расстояниями линзы. Они равны между собой, т.е. f₁ = f₂ = f, если слева и справа от линзы находится одна и та же среда ( воздух).

Экспериментальная установка и методы измерения

фокусных расстояний

Главное фокусное расстояние тонких линз можно измерить различными способами. Для этой цели используется установка, представленная на рис. 2. Установка состоит из оптической скамьи 1, на которой с помощью рейтеров 2 располагаются осветитель 3, исследуемая линза или система линз 4 и экран 5. Оптическая скамья снабжена шкалой для измерения положения осветителя, линз и экрана. В качестве предмета, изображение которого проектируется линзой на экран, используется сетка 6, расположенная в передней части осветителя.

Располагая на оптической скамье собирающую линзу, получим на экране действительное изображение предмета. При этом ход лучей в линзе имеет вид, представленный на рис. 3.

Рис. 2

Запишем формулы тонкой линзы (1)–(3)

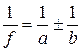, (1)

где f – главное фокусное расстояние линзы; а – расстояние от предмета до оптического центра линзы; b – расстояние от изображения до оптического центра линзы.

Из (1) следует, что

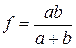. (2)

Очевидно, что формула (2) может быть использована как рабочая для определения главного фокусного расстояния собирающей тонкой линзы, для чего достаточно измерить лишь расстояния а и b. Следует, однако иметь в виду, что измеряя расстояния от предмета и изображения до оптического центра линзы, мы допускаем ошибку порядка толщины линзы. Поэтому измерение главного фокусного расстояния тонкой линзы имеет смысл только с точностью до ее толщины.

Пусть расстояние между предметом и экраном превышает 4f. Нетрудно убедиться, что в этом случае всегда найдутся два таких положения линзы (рис. 4), при которых на экране получаются отчетливые изображения предмета (в одном случае увеличенное, в другом – уменьшенное). Поскольку в обоих случаях изображения предмета на экране получаются с помощью одной и той же линзы, то на основе формулы (1) можно записать

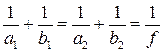(3)

или

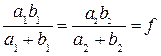. (4)

Но, как следует из рис. 4

а₁ + b₁ = а₂ + b₂ = L; (5)

а₁ – b₁ = а₂ – b₂ = l. (6)

Тогда с учетом (5) выражение (4) примет вид

а₁b₁ = а₂b₂, (7)

или, выразив а₂ и b₂ через l из (6), получим

а₁b₁ = (l + а₁)(b₁ – l), (8)

откуда следует, что

b₁ - а₁ = l. (9)

Таким образом, учитывая (5) и (9), составляем систему уравнений:

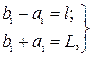(10)

решив которую, будем иметь:

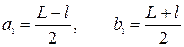. (11)

Подставляя эти значения а₁ и b₁ в формулу (3), находим

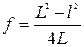. (12)

Формула (12) является рабочей для определения главного фокусного расстояния собирающей линзы методом Бесселя.