Определение главного фокусного расстояния
Собирающей линзы методом Бесселя
1. Установите экран на оптической скамье так, чтобы расстояние между ним и предметом было больше чем 4f (ориентировочно).
2. Расположите собирающую линзу между предметом и экраном так, чтобы на экране появилось резкое увеличенное изображение предмета. Запишите деление шкалы а1, соответствующее положению линзы на оптической скамье.
3. Переместите, не изменяя расстояния между осветителем и экраном, линзу вдоль оптической скамьи так, чтобы на экране появилось уменьшенное изображение предмета. Запишите деление шкалы а2, соответствующее новому положению линзы на оптической скамье.
4. Определите расстояние l как разность между двумя положениями линзы, т.е. l = a2 – a1.
5. Измерьте расстояние между предметом и экраном (однако оно должно оставаться больше чем 4f) и повторите опыт. Опыт повторить не менее трех раз. Результаты измерений занесите в табл. 2.
6. Рассчитайте фокусное расстояние собирающей линзы по методу Бесселя для всех трех опытов и найдите среднее значение. Результаты занесите в табл. 2.
Таблица 2
| № | L, см | а1, см | а2, см | l, см | f, см | 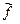 , см , см
|
Контрольные вопросы
1. Какой из двух рассмотренных в работе методов, определения главного фокусного расстояния собирающих линз является более точным? Почему?
2. Зависит ли главное фокусное расстояние линзы от длины волны падающего на него света? Если зависит, то, каким образом?
3. Что называют оптической силой линзы? Как изменится оптическая сила при погружении линзы в оптически прозрачную жидкость?
4. Что называют увеличением линзы? Изменится ли увеличение линзы при погружении ее в оптически прозрачную жидкость? Если изменится, то, каким образом?
ЛАБОРАТОРНАЯ РАБОТА № 13
ОПРЕДЕЛЕНИЕ СВЕТОВОЙ ВОЛНЫ С ПОМОЩЬЮ ДИФРАКЦИОННОЙ РЕЩЕТКИ
Цель работы:
1) Изучение интерференции и дифракции на дифракционной решетке;
2) Измерение длины световой волны.
Краткие сведения из теории
Явление интерференции и дифракции света
Свет – электромагнитная волна форма материи, проявляющая как волновые, так и корпускулярные свойства.
Волновые свойства света обнаруживаются в явлениях интерференции и дифракции. Интерференцией называется явление, сопровождающееся пространственным перераспределением интенсивности в области наложения только когерентных световых волн. Поэтому в этом случае наблюдаются устойчивые положения максимумов и минимумов световых волн. Интенсивностью световой волны называется величина, численно равная средней энергии, переносимой световой волной за единицу времени через единицу площади поверхности, перпендикулярной к падающему лучу. Интенсивность пропорциональна квадрату амплитуды падающей волны.
Когерентные волны – это волны с одинаковыми частотами колебаний, с постоянной во времени разностью фаз в точке наложения или с постоянной оптической разностью хода 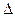 до точки наложения. Кроме того, в световых волнах должны быть одинаковыми направления колебаний.
до точки наложения. Кроме того, в световых волнах должны быть одинаковыми направления колебаний.
Максимум интенсивности при интерференции когерентных волн наблюдается, если оптическая разность хода равна: 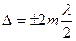 , а разность фаз
, а разность фаз 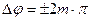 ., то есть колебания в исследуемую точку приходят в одинаковой фазе.
., то есть колебания в исследуемую точку приходят в одинаковой фазе.
Минимум интенсивности наблюдается, если 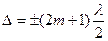 , и
, и 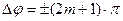 , то есть колебания в исследуемую точку приходят в противофазе. В данном случае m – целое число m = 0,1,2,3…
, то есть колебания в исследуемую точку приходят в противофазе. В данном случае m – целое число m = 0,1,2,3… 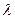 - длина волны в вакууме и в воздухе.
- длина волны в вакууме и в воздухе.
Явление дифракции возникает при нарушении целостности волновой поверхности и проявляется, в частности, в нарушении закона прямолинейного распространения света (проникновении света в область геометрической тени), то есть огибание волнами препятствий, соизмеримых с длиной падающей волны на это препятствие.
Задача дифракции заключается в нахождении распределения освещенности на экране в зависимости от размеров и формы препятствий. В большинстве случаев явление дифракции можно объяснить используя принцип Гюйгенса – Френеля.
Согласно принципу Гюйгенса, каждую точку, в которую пришла волна от источника, можно принять за центр вторичных волн. Френель дополнил и развил эту идею следующими положениями: вторичные волны когерентны и интерферируют при наложении.
Дифракция света в параллельных лучах называется дифракцией Фраунгофера (источник удален от экрана на большое расстояние). В данной работе изучается дифракция Фраунгофера. В этом случае дифракционная картина наблюдается в виде темных и светлых полос, если падает монохроматический свет, то есть свет с длиной волны 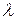 .
.
Дифракционная решетка
Рассмотрим систему N одинаковых щелей (рисунок.1) шириной а, разделенных одинаковыми непрозрачными промежутками b, такая система называется дифракционной решеткой 

Рисунок .1
Пусть свет падает на решетку нормально. За щелями в результате дифракции лучи будут распространяться под различными углами к лучам, падающими на решетку. Если на пути этих лучей поместить собирающую линзу, то в фокальной плоскости этой линзы в одной точке соберутся лучи, отклоненные под одинаковыми углами. Оптическая разность хода между соответствующими лучами от соседних щелей равна: 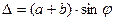 , где угол
, где угол 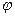 - это угол между направлением падающего луча на щель и отклонённым лучом при дифракции, или
- это угол между направлением падающего луча на щель и отклонённым лучом при дифракции, или 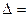 d sin
d sin 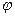 , где d = a+b - называется периодом дифракционной решетки, этой разности хода соответствует разность фаз
, где d = a+b - называется периодом дифракционной решетки, этой разности хода соответствует разность фаз 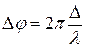 .
.
Если 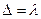 , то
, то 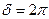 , следовательно, лучи придут в одинаковых фазах, и будут усиливать друг друга.
, следовательно, лучи придут в одинаковых фазах, и будут усиливать друг друга.
Условие образования максимумов в этом случае имеет вид: d sin 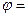 m
m 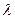 , где m = 0;
, где m = 0; 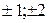 . Эти максимумы называются главными.
. Эти максимумы называются главными.
Из условия максимума следует, что при m=0, 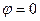 . На экране получается максимум нулевого порядка. При
. На экране получается максимум нулевого порядка. При 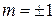 по обе стороны от нулевого возникают два дифракционных максимума первого порядка и так далее.
по обе стороны от нулевого возникают два дифракционных максимума первого порядка и так далее.
При освещении дифракционной решетки белым светом, полоса нулевого порядка белого цвета, так как для 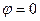 условие максимума выполняется для любых длин волн. Каждая полоса порядка m
условие максимума выполняется для любых длин волн. Каждая полоса порядка m 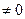 представляет собой спектр, причем красному его краю соответствует больший угол дифракции.
представляет собой спектр, причем красному его краю соответствует больший угол дифракции.
Интенсивность максимумов постепенно убывает, число дифракционных спектров ограничено и определяется условием
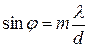
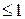 . (1)
. (1)
Дифракционная решетка является хорошим спектральным прибором, широко используется в спектроскопии, в частности, для измерения длин волн света.
Описание экспериментальной установки и метода измерений
Используемый в работе прибор состоит из линейки (1) с делениями, на одном конце которой закреплена дифракционная решетка (2), вдоль которой свободно может перемещаться экран со щелью и миллиметровой шкалой (3). (Рисунок 61.2).

Рисунок .2
Если на щель (4) направить пучок сета от источника, то посмотрев на нее через дифракционную решетку (2), по обе стороны от нее на шкале подвижного экрана (3) можно увидеть дифракционную картину - максимумы нескольких порядков, разделенные минимумами. Если свет белый, то максимумы будут представлять собой спектры белого света. Явление это объясняется следующим образом: на сетчатке глаза в фокальной плоскости хрусталика глаза собираются параллельные пучки лучей, отклоненные решеткой. Если угол отклонения ( 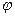 ) удовлетворяет условию d sin
) удовлетворяет условию d sin 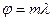 , то в точке Ф (рисунок 61.1) получается изображение щели, соответствующее длине волны
, то в точке Ф (рисунок 61.1) получается изображение щели, соответствующее длине волны 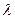 . Наблюдатель увидит это изображение на шкале на продолжении лучей, попавших в глаз.
. Наблюдатель увидит это изображение на шкале на продолжении лучей, попавших в глаз.
Из формулы d sin 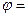 m
m 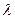 следует, что
следует, что 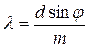 . (.2)
. (.2)


Рисунок 3
Для спектров малых порядков отклонения лучей угол мал, так как 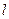 2
2 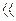
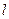 1 (рисунок 61.3), где
1 (рисунок 61.3), где
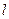 1 - расстояние, отсчитанное по линейке (1) от дифракционной решетки до экрана со щелью;
1 - расстояние, отсчитанное по линейке (1) от дифракционной решетки до экрана со щелью; 
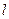 2 - расстояние от щели до выбранной линии спектра, отсчитанное по шкале подвижного экрана (3). (Рисунок 3).
2 - расстояние от щели до выбранной линии спектра, отсчитанное по шкале подвижного экрана (3). (Рисунок 3).
Тогда sin 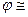 tg
tg 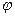 =
= 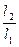 , откуда
, откуда
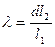 или
или 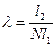 где
где 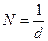 .
.
N – число щелей на единицу длины для данной дифракционной решетки.
Порядок выполнения работы
1 Перед началом работы устанавливают осветитель и, глядя на щель через дифракционную решетку, измеряют расстояние от щели до красных спектров первого и второго порядков ( 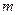
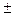 1,
1, 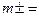 2), соответствующих самым длинным видимым красным лучам. Отсчет необходим для правого
2), соответствующих самым длинным видимым красным лучам. Отсчет необходим для правого 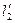 и левого
и левого 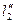 спектров, то есть по обе стороны от центрального максимума, для которого m=0 (белый свет). Из полученных данных определить среднее значение
спектров, то есть по обе стороны от центрального максимума, для которого m=0 (белый свет). Из полученных данных определить среднее значение
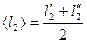 (3)
(3)
2 Измерить расстояние l1 от щели до дифракционной решетки.
3 Для еще двух значений l1 измерить соответствующее значение l2 для тех же красных лучей, то есть для m= 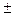 1; и m=
1; и m= 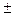 2.
2.
4 Найти значение 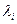 соответствующее различным значениям l1 и m по формуле
соответствующее различным значениям l1 и m по формуле
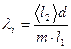 (4)
(4)
где 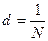 - постоянная дифракционной решетки, причем N – число штрихов на единицу длины N=105м-1.
- постоянная дифракционной решетки, причем N – число штрихов на единицу длины N=105м-1.
5 Вычислить абсолютную 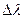 и относительную
и относительную 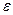 погрешности по формулам
погрешности по формулам
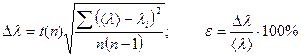 , (5)
, (5)
где t(n) – коэффициент Стьюдента для n, n – число измерений.
6 Результаты измерений и вычислений занести в таблицу.
Таблица измерений и вычислений
| № | 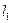
| 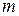
| 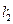
| 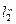
| 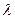
| 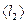
| 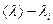
| 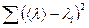
| 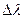
| 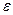
|
| м | м | м | м | м | м | м2 | м | % | ||
| ср. |
Записать результат измерений в виде доверительного интервала
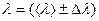
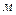 (6)
(6)
Контрольные вопросы
1. Что такое свет?
2. Какое явление называется интерференцией?
3. Перечислите признаки когерентных волн.
4. Укажите условия наблюдения максимума и минимума при интерференции.
5. Какое оптическое явление называется дифракцией света? Когда оно наблюдается?
6. В чем заключается принцип Гюйгенса, Гюйгенса-Френеля?
7. Как происходит дифракция света на дифракционной решетке?
8. Покажите ход лучей после решетки?
9. Опишите дифракционную картину от решетки. Запишите условия появления максимумов и минимумов.
10. Каков порядок следования цветов в дифракционных спектрах? Почему?
Дата добавления: 2015-02-03; просмотров: 1911;
