На другую частоту вращения
Предположим, что имеется характеристика насоса при частоте вращения п1, а двигатель этого насоса работает при частоте вращения п2, отличной от n1. Для того чтобы судить об эксплуатационных свойствах насоса, необходимо иметь его характеристику при той частоте вращения п2, при которой он фактически будет работать. Эту характеристику можно получить путем пересчета имеющейся характеристики на новую частоту врашения п2по формулам (5.40) - (5.42) и (5.39). Для этого задаются рядом значений додач Q1 и по имеющейся характеристике насоса находят соответствующий им напор Н1, мощность N1 и КПД η1 (рис. 5.21, стр. 235). Подставив найденные для частот вращения п1 величины Q1, Н1, N1 и η1 в уравнения (5.40)— (5.42) и (5.39), получают значения подачи Q2, напора Н2, мощности N2 и КПД η2, которые являются координатами точек характеристики насоса при частоте вращения п2. По этим координатам строят на характеристике ряд точек, соединив которые плавными кривыми, получают искомую характеристику насоса при частоте вращения п2.
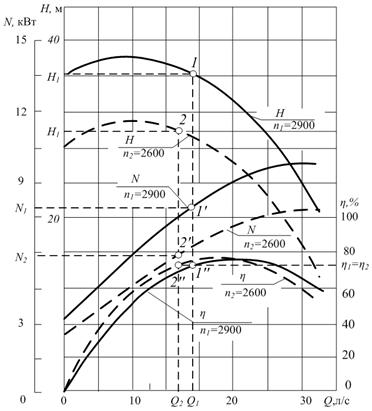
Рис. 5.21. Пересчет характеристики насоса на другую частоту вращения
Найдем в координатах Q – Н геометрическое место точек режимов, подобных режиму, который определяется точкой 1 (рис. 5.22, стр. 236). Для этого, подставив координаты Q1 и Н1 точки 1 в уравнения (5.40) и (5.41), определим папор и подачу при различных значениях частоты вращения. В результате найдем ряд точек: 2, 3, 4, ..., – соединив которые плавной линией, получим кривую подобных режимов работы насоса. Покажем, что эта кривая представляет квадратичную параболу с вершиной в начале координат. Для этого подставим в уравнение (5.41) значения п1/п2, найденные из уравнения (5.40),
Н1/Н2=(n1/n2)2=(Q1/Q2)2,
или
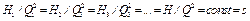 .
.
Следовательно, уравнение кривой подобных режимов имеет вид
H = sQ2. (5.43)
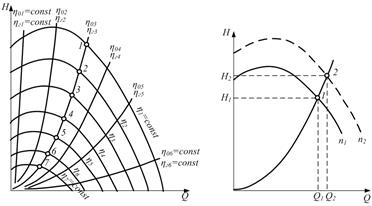
| Рис. 5.22. Кривые подобных режимов |
| Рис. 5.23. К определению частоты вращения, при которой характеристика проходит через заданную режимную точку |
Для подобных режимов гидравлический и объемный КПД с достаточной степенью точности можно считать одинаковыми. Следовательно, кривые подобных режимов являются также кривыми равных объемных и гидравлических КПД насоса. Механический КПД для подобных режимов не остается постоянным, поскольку механические потери складываются из потерь как на дисковое трение, так и на трение в уплотнениях вала и подшипниках. При возрастании частоты вращения мощность дискового трения увеличивается пропорционально гидравлической мощности (или частоте вращения в третьей степени), потери же на трение в уплотнениях вала и подшипниках растут вначительно медленнее, чем гидравлическая мощность. В результате при увеличении частоты вращения роль потерь на трение в уплотнениях вала и подшипниках в балансе энергии уменьшается, что приводит к увеличению механического и, следовательно, общего КПД.
Предположим, что от насоса требуется получить подачу Q2 при наноре Н2 и что режимная точка 2 с координатами Q2 и Н2 не лежит на характеристике насоса, полученной при частоте вращения n1 (рис. 5.23). Надо определить такую частоту вращения, при которой насос сможет обеспечить заданный режим работы, другими словами, определить такую частоту вращения n2, при которой кривая напоров Н = f (Q) характеристики пройдет через заданную точку 2 с координатами Q2 и Н2.
Искомую частоту вращения п2 можно определить, используя формулы (5.40) и (5.41) пересчета. Поскольку они справедливы только для подобных режимов, то для того чтобы можно было ими воспользоваться, необходимо найти такой режим (Q1, Н1) работы насоса при частоте вращения п1, который был бы подобен заданному режиму (Q2, Н2). Выше было показано, что подобные режимы работы насоса лежат на параболе подобных режимов Н = sQ2. Этому уравнению должны удовлетворять координаты заданной точки 2 и искомой точки 1. Положение точки 1 находим графическим путем. Для этого проводим через заданную точку 2 параболу подобных режимов. Пересечение параболы с кривой напоров Н = f (Q) при частоте вращения п1 дает режимную точку 1 с координатами Q1 и Н1 .Так как точки 1 и 2 лежат на одной и той же параболе подобных режимов, то режимы 1 и 2 подобны и для них справедливы формулы.
В этих формулах неизвестна только частота вращения п2, которую можно определить по любому из уравнений.
Дата добавления: 2015-01-29; просмотров: 1708;
