Коэффициент быстроходности

Выше было указано, что в настоящее время широко применяется проектирование нового насоса путем пересчета по формулам подобия размеров существующего насоса. Для того чтобы воспользоваться этим методом, следует выбрать среди всего многообразия существую­щих насосов, имеющих высокие технико-экономические показатели, такой насос, у которого режим, подобный заданному режиму работы проектируемого насоса, был бы близок к оптимальному. Для этого необходимо найти параметр, который служил бы критерием подобия и, следовательно, был бы одинаков для всех подобных насосов. Опре­делив по заданным Н, Q и n проектируемого насоса этот критерий по­добия и сравнив его с критериями подобия имеющихся конструкций, получим возможность подобрать необходимый насос.

В предыдущем параграфе было выяснено, что для подобных насо­сов, работающих на подобных режимах, справедливы уравнения.

Q₁/Q₂ = (n₁/n₂)( L₁/L₂)³ и Н₁/Н₂ = [n₁ L₁/(L₂n₂)] ² .

Эти уравнения можно записать иначе:

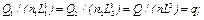(5.44)

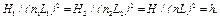(5.45)

Величины q и h одинаковы для подобных насосов, работающих в подобных режимах, и, следовательно, являются критериями по­добия. Однако они не могут быть определены для проектируемого насоса, так как неизвестен его размер L.

Для того чтобы исключить из уравнений (5.44) и (5.45) линейный размер L, возведем правую и левую части уравнения (5.44) во вто­рую степень, а уравнения (5.45) — в третью и разделим уравнения одно на другое:

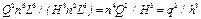
или

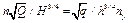. (5.46)

Как параметры q и h, так и п_y одинаковы для геометрически подобных насосов при работе их на подобных режимах независимо от плотности перемещаемой жидкости. Следовательно, параметр п_у является искомым критерием подобия. Его можно назвать удельной частотой вращения.

В насосостроении большее распространение получил параметр п_s, называемый коэффициентом быстроходности и в 3,65 раза больший удельной частоты вращения:

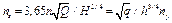. (5.47)

Коэффициент 3,65 не изменяет физического смысла n_s, который, так же как и п₇, является критерием (признаком) подобия насосов. Его происхождение историческое.

Входящие в уравнения (5.46) и (5.47) величины имеют следующие размерности: Q в м³/с, Н в м, п в об/мин.

Если насос, геометрически подобный данному, при подаче Q = 0,075 м³/с имеет напор 1 м, то согласно уравнению (5.47) его коэффициент быстроходности п₃ равен частоте вращения насоса. Действительно

.

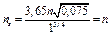На этом основании часто коэффициентом быстроходности называют ча­стоту вращения насоса, геометрически подобного данному, который при напоре 1 м подает 0,075 м³/с жидкости.

Коэффициент быстроходности различен для разных режимов ра­боты насоса. Назовем коэффициент быстроходности, определенный для оптимального режима, т. е. для режима, соответствующего мак­симальному значению КПД, коэффициентом быстроходности на­соса. Если насосы геометрически подобны, то коэффициенты быстро­ходности у них одинаковы. Следовательно, равенство коэффициен­тов быстроходности является необходимым признаком подобия насо­сов. Поскольку на заданные значения параметров п, Q_onт и Н_опт и, следовательно, для заданного значения коэффициента быстроход­ности можно сконструировать насосы с разными соотношениями раз­меров, равенство коэффициентов быстроходности не является доста­точным признаком геометрического подобия насосов. Однако прак­тикой установлены для каждого коэффициента быстроходности соот­ношения размеров насоса, обеспечивающие оптимальные технико-экономические показатели. Если ограничиться лишь этими, чаще всего применяющимися в насосах соотношениями размеров, то равенство коэффициентов быстроходности становится не только необходимым, но и в известной степени достаточным признаком (кри­терием) геометрического подобия насосов.

В зависимости от коэффициента быстроходности рабочие колеса лопастных насосов можно разделить на следующие разновидности (табл. 5.1).

1. Центробежные. Центробежные насосы бывают тихоходными и нормальными. Тихоходные насосы имеют малый коэффици­ент быстроходности (n_s = 50 ÷ 90). Из уравнения (5.47) следует, что при постоянной подаче и частоте вращения (чему соответствует постоянный диаметр горловины рабочего колеса D_o)коэффициент быстроходности тем меньше, чем больше напор. Чтобы получить большой напор, необходимо иметь большой диаметр D₂ рабочего колеса, поэтому тихоходные рабочие колеса имеют большое отно­шение D₂/D₀ диаметров, доходящее до трех. Лопатки рабочего ко­леса обычно имеют простую цилиндрическую форму с образующей цилиндра, параллельной оси насоса.

Нормальными являются колеса, имеющие п_а = 80 ÷ 300. Увеличение быстроходности, связанное с уменьшением на­пора, ведет к уменьшению выходного диаметра рабочего колеса (D₂/D₀ = 2,5 ÷ 1,4). Для уменьшения гидравлических потерь на входе в рабочее колесо, значение которых в общем балансе энергии возрастает по мере уменьшения напора насоса, входной участок лопаток выполняется двойной кривизны. Выходной участок имеет цилиндрическую форму.

2. Полуосевые (n_s = 250 ÷ 500; D₂/D_o = 1,4 ÷ 0,9). Уменьшить отношение D₂/D₀ до значения, близкого или меньшего единицы, можно только в том случае, если выходную кромку лопаток накло­нить к оси. Кроме того, наклон выходной кромки обеспечивает более плавную форму лопатки, что уменьшает гидравлические по­тери в рабочем колесе. Чтобы получить на разных струйках, имею­щих разный диаметр выхода, одинаковый напор, приходится лопатку выполнять двойной кривизны не только на входе, но и на выходе.

3. Осевые, или пропеллерные (п_s = 500 ÷ 1000; D₂/D₀ ≈ 0,8). При дальнейшем увеличении быстроходности наклон выходной кромки лопаток возрастает, и она становится почти перпендикулярной к оси насоса. При этом частицы жидкости движутся через рабо­чее колесо приблизительно на постоянном расстоянии от его оси. В отличие от большинства центробежных насосов, колесо осевого насоса не имеет наружного обода.

По мере увеличения коэффициента быстроходности кривая напоров H = f (Q) становится более крутой. Мощность при подаче, равной пулю, увеличивается с ростом быстроходности. Если у насосов с ти­хоходными и нормальными колесами мощность возрастает с увеличе­нием подачи, то у насосов с полуосевыми колесами она почти не из­меняется с изменением подачи, а у насосов с осевыми колесами с уве­личением подачи уменьшается. Чем больше коэффициент быстроход­ности, тем круче падает кривая КПД по обе стороны от оптимального режима и, следовательно, тем меньше становится диапазон подач, в котором работа насоса экономически выгодна. Однако из-за увели­чения крутизны кривой напоров характеристики диапазон оптималь­ных напоров при увеличении быстроходности возрастает.

Так как напор лопастного насоса не зависит от рода перекачи­ваемой жидкости, удельная частота вращения и коэффи­циент быстроходности также не зависят от рода жидкости.

Многоступенчатый насос представляет собой несколько последо­вательно соединенных одноступенчатых насосов (ступеней), поэтому для него принято определять коэффициент быстроходности ступени, а не всего насоса, для чего в уравнения (5.46) и (5.47) следует подстав­лять напор одной ступени.

Рабочее колесо насоса двустороннего входа можно рассматри­вать как два параллельно соединенных колеса, поэтому при определе­нии коэффициента быстроходности такого насоса значение подачи, входящее в уравнения (5.46) и (5.47), следует брать равным Q/2, где Q — подача насоса.