Давление жидкости на цилиндрическую стенку
Задача нахождения силы давления жидкости на поверхность произвольной формы является достаточно сложной задачей. Эта задача решается, как правило, графическим методом путем построения эпюры гидростатического давления.
Однако на практике чаще всего приходится иметь дело с цилиндрическими или сферическими поверхностями, имеющими вертикальную плоскость симметрии, например стенки труб, резервуаров и всевозможных цилиндрических сосудов, шаровыми клапанами. Сила давления в этом случае может быть найдена аналитическим путем.
Рассмотрим цилиндрическую стенку АВ шириной b (перпендикулярно к плоскости чертежа) и определим силу давления жидкости на эту стенку (рис. 2.31).
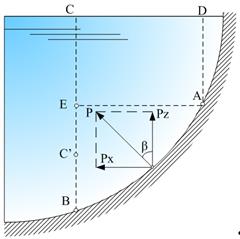
Рис. 2.31.Расчетная схема давления жидкости на цилиндрическую
поверхность сверху
Проведем из точек А и В перпендикуляры AD и ВС к свободной поверхности жидкости. Объем жидкости в отсеке ABCD называется телом давления. Жидкость в этом объеме находится в равновесии, поэтому составим обычные условия равновесия в вертикальном и горизонтальном направлениях.
Если жидкость действует на поверхность АВ с силой Р, то и поверхность АВ действует на жидкость с силой Р, направленной в обратную сторону. Эту силу реакции разложим на две составляющие: горизонтальную Рx и вертикальную Рz.
На выделенный объем жидкости сверху вниз действуют следующие силы: сила давления на свободной поверхности жидкости равная произведению поверхностного давления p0 на площадь горизонтальной проекции поверхности АВ, и сила тяжести жидкости в объеме ABCD. Эти две силы уравновешиваются снизу вертикальной составляющей Рв, В связи с этим условие равновесия рассматриваемого объема в вертикальном направлении имеет вид:
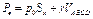 (2.37)
(2.37)
где Sx - площадь горизонтальной проекции поверхности АВ; VABCD – выделенный объем жидкости.
Если давление p0 на свободной поверхности жидкости равно атмосферному и находится сила избыточного давления, то очевидно, что
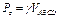 , (2.38)
, (2.38)
т. е. вертикальная составляющая силы избыточного давления жидкости на криволинейную стенку равна весу жидкости в объеме тела давления.
Для нахождения горизонтальной составляющей силы давления Рx проведем из точки А горизонтальную линию до пересечения с линией ВС в точке Е. Легко видеть, что горизонтальные силы давления жидкости на поверхности ЕС и AD взаимно уравновешиваются и остается лишь сила давления на площадь ВЕ, которая для равновесия выделенного объема жидкости должна быть равна горизонтальной составляющей Рx. Из рисунка видно, что площадь ВЕ представляет собой вертикальную проекцию поверхности АВ. Таким образом, с учетом сказанного, условие равновесия объема жидкости ABCD в горизонтальном направлении запишется в виде
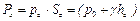 (2.39)
(2.39)
где pc - гидростатическое давление жидкости в центре тяжести площади ВЕ, т. е. в точке C’, hc’, - глубина расположения центра тяжести площади ВЕ; ωB - площадь вертикальной проекции поверхности АВ.
Горизонтальная составляющая силы избыточного давления жидкости при pо= pа равна
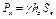 (2.40)
(2.40)
Полная сила гидростатического давления, являющаяся равнодействующей ее составляющих Рв и Рг, определяется зависимостью:
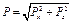 (2.41)
(2.41)
а ее направление – углом β, значение которого может быть определено из выражения:
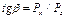 ( 2.42)
( 2.42)
Когда жидкость расположена снизу от стенки гидростатическое давление во всех точках поверхности АВ имеет те же значения, что и в рассмотренном случае, но направление силы будет противоположным, и составляющие силы Рz и Рx определяются по тем же формулам (2.37) и (1.39), но с обратным знаком. При этом при вычислении Рz также определяется вес жидкости в объеме тела давления ABCD, этот объем и не заполнен жидкостью и поэтому называется фиктивным телом давления.
Рассмотрим другой пример и определим давление на стенку цилиндрического сегментного щита, служащего для выпуска воды из турбинных аванкамер (рис. 2.32).
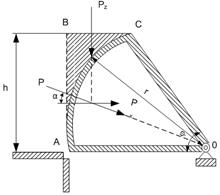
Рис. 2.32. Давление на стенку цилиндрического сегментного щита
Горизонтальная составляющая силы полного давления на такую стенку будет равна давлению на вертикальную проекцию этой стенки, т. е. на плоскость, размер которой по высоте равен h (глубине) и по ширине равен ширине щита b.
Таким образом, проекция полного давления на ось Х равна на основании предыдущего
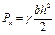 (2.43)
(2.43)
Для определения вертикальной слагающей полного давления необходимо определить вес жидкости в объеме заштрихованной фигуры, изображающей столб жидкости, расположенный над стенкой. Этот объем равен умноженной на ширину щита b площади криволинейной фигуры АВС, величина которой в свою очередь может быть найдена как разность площадей трапеции ОАВС и кругового сектора ОАС.
Итак: 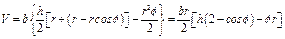
При этом очевидно: 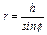
Отсюда 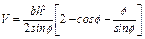 и, следовательно, вертикальная слагающая силы полного давления
и, следовательно, вертикальная слагающая силы полного давления
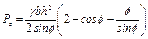 (2.44)
(2.44)
Так как все истинные давления, действующие на щит, перпендикулярны его поверхности (а, следовательно, направлены по радиусам), то они образуют систему сходящихся в одной точке сил и их равнодействующая будет проходить обязательно через ось вращения щита, т. е. через точку О. Таким образом, величина полного давления на щит будет равна:
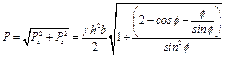
а тангенс угла наклона этой силы к горизонту будет равен
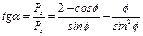
Если 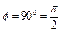 , то
, то 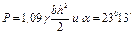
Дата добавления: 2015-01-29; просмотров: 2700;
