Пьезометры, манометры и вакууметры

В том случае, когда давле­ние в жидкости измеряют не­посредственно высотой столба той же самой жидкости, такой прибор называют пьезометром.

Величину, получающуюся в результате деления давления на удельный вес жидкости, называют пьезометрической высотой (от греч. 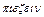(пьедзейн) - «давить»):

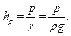(2.17)

Размерность h_p характе­ризуется только линейными единицами:

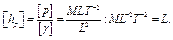
Пусть жидкость в точке О сосуда S (рис.2.14) находится под избыточным давлением p_о. Очевидно, что если при этом в стенке сосуда будет сделано отверстие, то жидкость будет бить оттуда фонтаном. Если же отверстие будет соединено с достаточно высокой вертикальной трубкой, то жидкость под действием давления подни­мется по этой трубке вверх.

Высота подъема жидкости в трубке будет ограничена, так как при дости­жении некоторого уровня наступит равновесие: вес столба жидкости в вертикальной трубке уравнове­сит давление внутри сосуда S. Определим эту предельную высоту h_p , на которую поднимется жид­кость под избыточным давлением p_о. Расположим оси координат так, чтобы начало совпадало с осно­ванием трубки и ось Z была направлена по вертикали вверх.

Тогда имеем:

1) в точке О координата z = 0; избыточное давле­ние p = p_о;

2) в точке а координата z= h_p; избыточное да­вление p=0; по определению 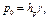откуда

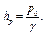
Таким образом, пьезометрическая высота - это та высота, на которую поднимается жидкость в верти­кальной трубке благодаря внутреннему давлению.

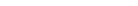Принимая во внимание сказанное, уравнение (1) можно переписать следующим образом:

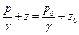(2.18)

Основное уравнение гидростатики в этом случаю формулируется так: для всякой точки покоящейся жидкости сумма пьезометри­ческой и нивелирной высот есть величина постоянная.

Таким образом, если в произвольном сосуде (рис.2.15, стр. 76) жидкость находится в покое и в точке а (координата которой равна z₁) давление будет p₁, в точке b(z₂) давление p₂ и в точке c(z₃) гидростатическое давление равно p₃, то на основании уравнения (2.18) можно написать:

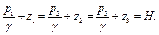
При этом уровни во всех трех пьезометрических трубках расположены на одной высоте. Отсюда следует, что в открытых сообщающихся сосудах в случае покоя однородная жидкость располагается на одной и той же высоте.

На рисунке (рис. 2.16, стр. 76) видно, что суммарная высота Н для всякой точки делится этой точкой на два отрезка. Первый, расположенный ниже точки, представляет собой нивелирную высоту этой точки, второй, расположенный выше точки, - пьезометриче­скую высоту.

Координата z называется нивелирной или гео­метрической высотой, слагаемое р/γ имеет линейную размерность и называется пьезометрической высотой. Пьезометриче­скую высоту, соответствующую избыточному давлению, можно наблюдать в открытой сверху стеклянной трубке, которая называет­ся пьезометром открытого типа.

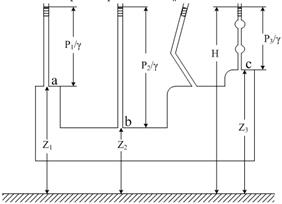
Рис. 2.15. Геометрический смысл основного уравнения гидростатики

Для открытого сосуда абсолютное давление в жидкости на уровне присоединения пьезометра:

p_абс = p_а + γh_п,

где p_а - атмосферное давление; h_п - высота подъема жидкости в пьезо­метре.

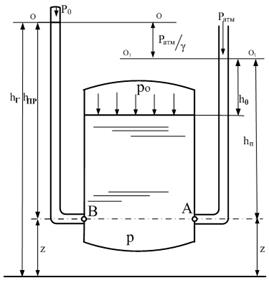
Рис. 2.16. Пьезометрический и гидростатический напор

Отсюда высота подъема жидкости в пьезометре равна:

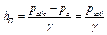(2.19)

где p_изб – избыточное давление в жидкости на уровне присоеди­нения пьезометра.

Очевидно, что если на свободную поверхность жид­кости в сосуде действует атмосферное давление, т. е. p_о = p_а, то уровни в сосуде и пьезометре будут одинако­вы, т. е. пьезометрическая высота для любой точки рас­сматриваемого объема жид­кости будет равна глубине расположения этой точки под свободной поверхностью жид­кости.

Пьезометрическая высота, соответствующая абсолютному дав­лению в данной точке жидкости, называется приведенной высотой. Приведенную высоту можно наблюдать в закрытой сверху стеклян­ной трубке, из которой удален воздух. Такая трубка называется закрытым пьезометром.

Применив формулу (2.19) к жидкости, заключенной в закрытом пьезометре, который присоединен в точке В, получим

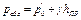
где p_абc – абсолютное давление в точке В; p – внешнее давление на сво­бодную поверхность жидкости в пьезометре; h_ПР - приведенная высота.

Предположим, что 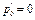, т. е. в верхнем конце закрытой труб­ки имеется физический вакуум. Тогда

p_абс = γh_ПР,

откуда

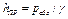(2.20)

Очевидно, что приведенная высота h_пр всегда будет больше пьезо­метрической высоты h_п, соответствующей избыточному давлению на величину, равную высоте столба жидкости, соответствующей атмосферному давлению, т. е.

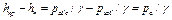
Часто давление в жидкостях или газах численно выражают в виде соответствующей ему пьезометрической высоты жидкостного столба по формуле:

h = р/γ_ж.

Например, 1 ат соответствуют:

для водного столба:

;

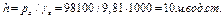для ртутного столба:

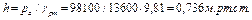
Сумма пьезометрической h_п и геометрической z высот называется пьезометрическим напором Н_п в данной точке жидкости по отно­шению к какой - либо горизонтальной плоскости OO (плоскости срав­нения), т. е.

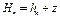(2.21)

или

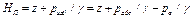(2.22)

Сумма приведенной высоты давления h_пp и геометрической вы­соты положения z рассматриваемой точки относительно произволь­ной плоскости сравнения называется гидростатическим напором Н_г в данной точек жидкости, т.е.

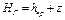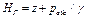, (2.23)

Для пьезометрического напора получим:

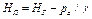(2.24)

Таким образом, отличие пьезометрического напора от гидро­статического заключается в учете противодавления атмосферы. Так как в большинстве случаев практики приходится иметь дело с избыточным давлением, измеряемым открытым пьезометром, то для практики понятие пьезометрического напора имеет большее значение, чем понятие гидростатического напора.

Выражая абсолютное давление по основному уравнению гидростатики

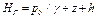(2.25)

Так как давление на свободной поверхности жидкости в сосуде p₀ и сумма высот z + h одинаковы для любой точки жидкости, то

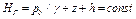
т. е. гидростатический напор для всех точек покоящейся жидкости есть величина постоянная.

В какой бы точке жидкости не был установлен закрытый пьезо­метр, жидкость поднимается в нем до одного и того же уровня. Этот уровень образует горизонтальную плоскость О-О (см. рис.), которая называется плоскостью гидростатического напора.

Так как атмосферное давление p_а не зависит от положения рас­сматриваемой точки в жидкости, то, учитывая формулу (2.24), можно заключить, что и пьезометрический напор Н_п во всех точках покоящейся жидкости одинаков, т. е.

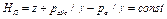
Отсюда следует, что и уровни пьезометрических высот для всех точек покоящейся жидкости лежат в одной и той же горизон­тальной плоскости О₁ –О_1, которая называется плоскостью пьезо­метрического напора.

Если давление на свободной поверхности жидкости p_о ока­жется меньше атмосферного, то плоскость пьезометрического напора будет расположена ниже уровня свободной поверхности жидкости в сосуде на величину h_вак. В этом случае все частицы жидкости в сосуде, расположенные ниже плоскости О₁ –О_1, будут иметь абсолютное давление, большее атмосферного, а расположенные выше этой плоскости – меньшее атмосферного. Если абсолютное давление в жидкости меньше атмосферного, то говорят, что имеется разрежение, или вакуум. За разрежение, или вакуум, принимается недостаток давления до атмосферного:

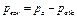
или

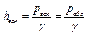
Справедливо, что р_вак = - р_изб, т. е. вакуум выражает собой отрицательное избыточное давление.

Так как нижним пределом для абсолютного давления в жидкости является нуль, то максимальное значение вакуума численно равно атмосферному давлению, т.е. максимальная вакуумметрическая высота

.

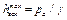Вакуум в жидкости измеряется с помощью приборов, называе­мых вакуумметрами. Простейшие вакуумметры представляют собой либо U-образные трубки, либо перевернутые U-образные трубки, один конец которых опущен в сосуд с жидкостью (рис. 2.17).

Для измерения давления жидкостей помимо пьезометров используют манометры, которые делятся на жидкостные и ме­ханические.

С помощью пьезометра можно определять сравнительно небольшие избыточные давления (или небольшую разность давлений). Причем, чем меньше плотность жидкости в приборе, тем выше требуется стеклянная трубка для измерения давления. Так например, для измерения атмосферного давления в единицах водного столба потребуется трубка высотой 10м, а в единицах ртутного столба – 0,760 м.

Поэтому для измерения больших давлений пользуются жидкостными манометрами, в которых столбом, уравновешивающим измеряемое давление, является столб ртути.

Манометр представляет собой U – образную трубку, заполненную ртутью (рис.2.17, стр. 80). Под давлением жидкости, находящейся в сосуде О, ртуть в левом колене понизится, а в правом поднимется и займет положение ab. Зная расположение уровней а, b и О относительно какой-нибудь вертикальной шкалы, можно легко определить давление на уровне О. В самом деле, так как про­странство Оа заполнено однородной жидко­стью (удельного веса γ_ж), находящейся в покое, то для этого случая справедливо бу­дет написать уравнение:

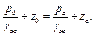
Точно так же, как пространство аb за­полнено однородной жидкостью, например ртутью (удельный вес которой обозначим γ_р), для этого участка можно написать:

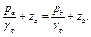
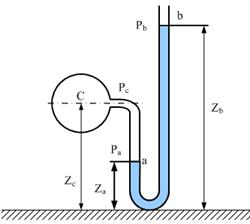
Рис.2.17. Жидкостный манометр

Из этих двух уравнений остается исключить давление p_а - давле­ние на поверхности раздела жидкости и ртути (в точке а):

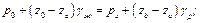
откуда определится искомое давление на уровне O:

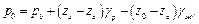
В том случае, когда в сосуде О находится газ, γ_ж мало по сравне­нию с γ_р и с большой степенью точности можно написать:

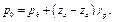(2.26)

Если конец манометрической трубки открыт в атмосферу, то избыточное давление р_b = 0.

Жидкостные ртутные манометры такого рода можно употреблять для измерения также не особенно больших давлений. Действительно, полагая 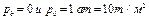, а также 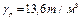, найдем

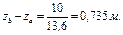
т. е. каждая атмосфера уравновешивается столбом ртути высотой 735 мм. Таким образом, уже при измерении давления порядка 5-6 ат в помещениях нормальных габаритов встретятся непреодолимые трудности.

В тех случаях, когда большое давление все же необходимо измерить жидкостным (ртутным) манометром, прибегают к много жидкостным манометра, один из которых изображен на рис. 2.18 (стр.82).

Такой манометр состоит из нескольких U – образных трубок, соединенных последовательно. Участки ab, cd и ef заполнены ртутью, а Oa, bc и de – какими-нибудь жидкостями (часто той же жидкостью, которая заполняет сосуд O). В этом случае для каждого участка можно написать уравнение типа (2.26).

Итак, имеем:

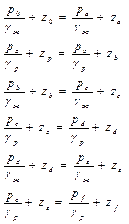(2.27)

Из этой системы уравнений можно исключить давления

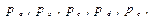
тогда искомое давление p₀ будет равно:

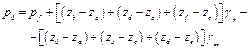
Для измерения больших давлений часто пользуются пружинными манометрами. Устройство одного из них показано на рис. 2.19 (стр. 82). Полая латунная трубка эллиптического сечения, имеющая форму серпа и закрытая с одного конца, сообщается другим концом с измеряемым объектом. Под давлением эта трубка стремиться разогнуться, и при этом приводит в движение зубчатую передачу, соединенную со стрелкой. Поворот стрелки на тот или иной угол можно фиксировать по шкале, которая градуирована на атмосферы и их доли.

Для измерения давления ниже атмосферного употребляются так называемые вакуумметры.

Вакуумметр представляет собой U - образную трубку, заполненную ртутью и сообщенную одним концом с измеряемым объектом. Пусть в сосуде О давление ниже атмосферного; тогда ртуть в левом колене поднимется выше, чем в правом. Нетрудно установить, что прин­ципиально вакуумметр ничем не отличается от манометра. Уравнения, написанные нами для манометра, останутся справедливыми и для данного случая, но так как здесь z_a >z_b, то

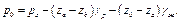(2.28)

Таким образом,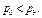

Разность между атмосферным давлением и остаточным абсолютным давлением, определяемым формулой (2.28) 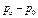называют разрежением или вакуумом.

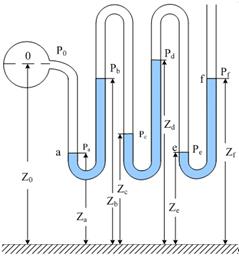
Рис. 2.18. Многожидкостный манометр

Естественно, что минимальная величина вакуума, которая поддается измерению ртутным вакуумметром, не может быть меньше, чем упругость паров ртути при температуре измерения.

На рис. 2.19 показаны схемы­ жидкостных манометров.

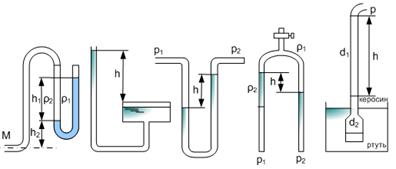
а) б) в) г) д)

Рис. 2.19. Схемы жидкостных нанометров

Так называемый U – образный манометр (рис. 2.19, а) представляет собой изогнутую стеклян­ную трубку, содержащую ртуть. При измерении небольших давлении газа вместо ртути применяют спирт, воду или другие жидкости. При измерении давления таким манометром следует учитывать высоту его расположения над точкой А, в которой измеряет­ся давление, так как избыточное давление в точке А

.

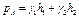Чашечный манометр (рис. 2.19, б) удобнее предыдущего тем, что позволяет фиксировать лишь один уровень жидкости.

Для измерения разности давлений в двух точках служат диффе­ренциальные манометры, простейшим из которых является U-образный манометр (рис. 2.19, в), заполненный ртутью. Разность давлений p₁ и p₂ в жидкости с удельным весом γ, замеренная таким манометром, определяется по формуле

.

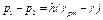Для измерения малых разностей давления жидкости применяют двухжидкостные микроманометры, представляющие собой перевер­нутую U-образную трубку с маслом или керосином в верхней ча­сти (рис. 2.19, г). Для этого случая

.

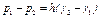Если абсолютное давление в жидкости или газе меньше атмосферного, то говорят, что имеет место разрежение, или вакуум.

За величину разрежения, или вакуума, принимается недостаток до атмосферного давления:

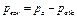или .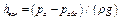

Возьмем, например, трубу с плотно пригнанным к ней поршнем, опустим нижний её конец в сосуд с жидкостью и будем постепенно поднимать поршень (рис. 2.20). Жидкость будет следовать за поршнем и вместе с ним поднимется на некоторую высоту h от свободной поверхности с атмосферным давлением.

Так как для точек, расположенных под поршнем, глубина погружения относительно свободной поверхности отрицательна, абсолютное давление жидкости под поршнем

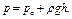, (2.29)

а вакуум

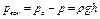или .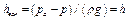

По мере подъема поршня абсолютное давление жидкости под ним уменьшается. Нижним пределом для абсолютного давлении в жидкости является нуль, а максимальное значение вакуума численно равно атмосферному давлению, поэтому максимальную высоту всасывания 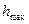жидкости можно определить из уравнения (2.29), если в нем положить р = 0 (точнее р = р_н.п.)_.

Таким образом, без учёта давления р_н.п. насыщенных паров

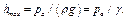
Простейшим устройством для измерения вакуума может служить стеклянная трубка, показанная на рис. 2.19 в двух вариантах. Вакуум в жидкости А можно измерять при помощи U – образной трубки (см. рисунок слева) или перевернутой U – образной трубки, один конец которой опущен в сосуд с жидкостью (см. рисунок справа).

Для измерения давлений более 0,2-0,3 МПа применяют механические манометры – пружинные или мембранные. Принцип их действия основан на деформации полой пружины или мембраны под действием измеряемого давления. Через механизм эта деформация передается стрелке, которая показывает величину измеряемого давления на циферблате. Схема пружин­ного манометра показана на рис. 2.21 (стр. 85). Он состоит из корпуса 1, шкалы 2, латунной трубки - пружины эллиптического сечения 3, стрелки 4 и передаточного механизма 5. Свободным концом труб­ки 3 манометр подсоединяется к жидкости в точке, где измеряется давление. При изменении давления трубка 3 стремится разогнуться или сжаться. Через передаточный механизм 5 эта деформация труб­ки передается стрелке, которая показывает значение измеряемого давления на шкале. По этому же принципу устроены и металличе­ские вакуумметры, устанавливаемые на всасывающих трубах центро­бежных насосов, сифонах и т.п.

Наряду с механическими манометрами применяют электрические манометры. В качестве чувствительного элемента (датчика) в электроманометре используют мембрану. Под действием измеряемого давления мембрана деформируется и через передаточный механизм перемещает движок потенциометра, который вместе с указателем включен в электрическую схему.

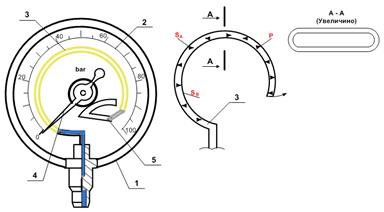
Рис. 2.21. Манометр пружинный