Опис лабораторної установки і методика вимірювання

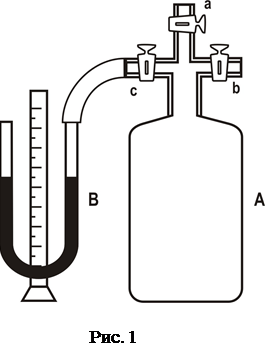
Для визначення відношення теплоємностей 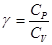повітря, що знаходиться в балоні, з ним проводять послідовність термодинамічних процесів, представлених на рV-діаграмі, рис.2.

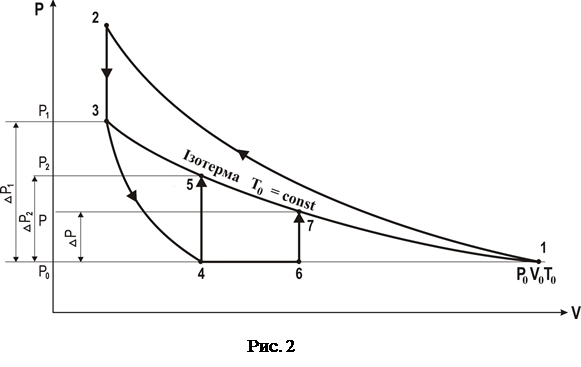
Позначимо через Р₀ , V₀ , T₀ вихідні величини термодинамічних параметрів газу в балоні. Спочатку в балон накачується повітря (процес 1®2 ). При цьому газ в балоні стискається і нагрівається. Потрібен деякий час на вирівнювання температури повітря всередині балону з температурою оточуючого середовища. Після ізохоричного охолодження до початкової кімнатної температури Т₀ (процес 2®3) газ має деякий тиск Р₁, а на манометрі встановиться певна різниця висот рівнів h₁.

Потім краном а з’єднують балон з атмосферою і газ адіабатично розширюється (процес 3®4). Газ при цьому охолоджується, його тиск падає до величини атмосферного Р₀ , а температура – до величини Т₁< Т₀.

В момент досягнення тиску Р₀ кран а перекривається, і газ ізохорично нагрівається до кімнатної температури Т₀ (процес 4®5). В кінцевому стані тиск газу Р₂ > Р₀, а на манометрі встановиться різниця висот рівнів рідини h₂ < h₁.

Маса газу, що знаходиться в балоні, в початковому стані виражається співвідношенням

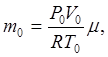(1)

Протягом всіх термодинамічних процесів маса газу в балоні більше або дорівнює m₀. Назвемо масу m₀ робочою масою газу. Ця маса повинна весь час залишатися в балоні. Газ, що накачується і випускається з балону, служить лише для стискання і розширення робочої маси газу m₀.

Введемо позначення DР₁ = Р₁ – Р₀ і DР₂ = Р₂ – Р₀. Оскільки перехід з 3-го в 4-й стан здійснюється адіабатично, то можна записати:

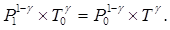(2)

Перехід з 4-го стану в 5-й здійснюється ізохорично, отже:

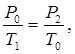(3)

Виключивши з рівнянь (2) і (3) температуру Т₁ і скоротивши потім на 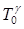, отримаємо

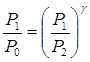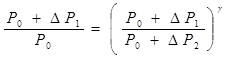
або (4)

Розв’яжемо рівняння (4) відносно показника адіабати:

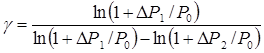. (5)

У роботі завжди виконується умова 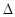P₁, 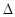P₂ << P₀ , що еквівалентно умові 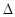P₁/P₀, 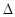P₂/ P₀ << 1. Остання умова дозволяє з точністю до членів другого порядку малості ( 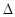P₁/P₀)² замінити у (5) логарифми – першими членами їх розкладу у ряди Тейлора, тобто відповідно:

ln( 1 + 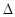P₁/P₀)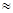 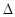P₁/P₀; ln( 1 + 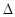P₂/P₀)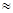 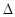P₂/P₀ .

Таким чином, отримаємо:

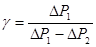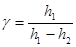або (6)

Отже, при такому методі розрахунку необхідно виконання наступних умов:

1. В процесі 3®4 кран балону повинен бути перекритий в момент, коли тиск в балоні буде дорівнювати Р₀.

2. Час, протягом якого тиск в балоні зменшується від Р₁ до Р₀ , повинен бути достатньо малим, так щоб теплообміном з оточуючим повітрям можна було знехтувати.

Розглянемо вплив часу t, протягом якого кран а ще залишається відкритим після досягнення тиску Р₀, на результат дослідження.

Припустимо, що після досягнення тиску Р₀ кран залишається відкритим ще деякий час t. За цей час відбувається ізобаричне нагрівання (процес 4®6) за рахунок теплообміну газу зі стінками балону, а також вихід частини газу з балону, викликаний нагріванням і розширенням цього газу. Величину t назвемо часом затримки.

Після того, як кран а закривається (точка 6), відбувається ізохоричне нагрівання (процес 6®7). Тиск в балоні досягає величини Р₀ + DР. Кінцевий стан: точка (7) лежить на тій самій ізотермі, що і точки 1, 3 і 5, але DР < DР₁.

З цього розгляду видно, що DР залежить від часу затримки t. Таким чином, якщо прийняти до уваги теплообмін і вихід частки газу з балону за час t, то g, розраховане за формулою (7), буде мати велику похибку.

Розглянемо детальніше процес охолодження протягом часу t. Рівняння балансу енергії для газу, що знаходиться в балоні, може бути записано у вигляді

- m с_P d T = a S (T – T₀) d t, (10)

де с_P – питома теплоємність газу; a - коефіцієнт тепловіддачі з поверхні балону;

m – змінна маса газу в балоні ( 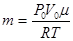); Т – температура газу в момент часу t; S – площа поверхні балону з повітрям.

Розв’язуючи це рівняння, отримаємо вираз:

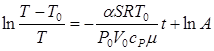
Константу інтегрування А знайдемо з умови: при t = 0 Т₁ = Т₀ - DТ₁. Кінцеве співвідношення буде мати вигляд:

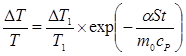. (11)

Температура газу Т тим більша, чим більший час витримки t. Після того, як в момент часу t кран а перекривається, нагрівання газу в балоні продовжується ізохорично. Тиск газу остаточно досягає величини

Р = Р₀ + DР.

З умови ізохоричності виходить, що

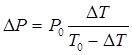, (12)

Для малих DР₁ і DТ₁ з рівняння адіабатичного процесу (3®4) виходить співвідношення: 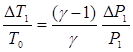(13)

Підставляючи співвідношення (12) і (13) в (11) і нехтуючи членами другого порядку малості, отримуємо формулу

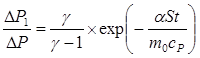, (14)

Це відношення враховує як теплообмін, так і вихід частини газу з балону в процесі нагрівання. Співвідношення (14) дозволяє знайти g за виміряними при різних величинах t значеннями DР₁ і DР. Графік залежності 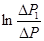від часу витримки t є лінійною функцією. Якщо екстраполювати цей графік до t = 0, то він буде відсікати на осі ординат відрізок: 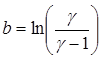, (15)

З рівняння (15) легко знаходиться відношення теплоємностей

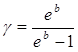, (16)