Трение на наклонной поверхности

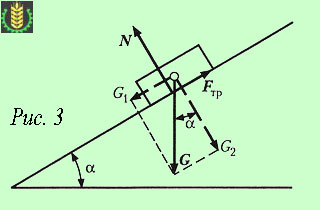Рассмотрим тело, лежащее на шероховатой наклонной плоскости, составляющей угол α с горизонтальной плоскостью (см. рисунок 3).Разложим силу тяжести тела G на составляющие G₁ и G₂, параллельную и перпендикулярную наклонной плоскости. Модули этих составляющих определим, используя тригонометрические зависимости:

G₁ = G sinα; G₂ = G cosα.

Составляющая G₁ стремится сдвинуть тело вдоль наклонной плоскости. Полностью или частично эта составляющая уравновешивается силой трения; согласно второму закону трения скольжения, ее максимальное значение равно:

F_тр = fN = fG cosα,

где f – коэффициент трения скольжения тела по наклонной плоскости.

Для того, чтобы тело, лежащее на наклонной плоскости, находилось в равновесии, движущая сила G₁ должна быть по модулю равна силе трения F_тр ,т. е.

G sinα = fG cosα или tgα = f = tgφ, откуда следует, что α = φ.

Если угол, который наклонная плоскость составляет с горизонтом, будет равен углу трения, то тело, лежащее на наклонной плоскости ,будет под действием собственной силы тяжести либо равномерно скользить вниз, либо находиться в состоянии покоя (что, собственно, одно и то же).

Для того, чтобы тело, лежащее на наклонной плоскости, заведомо не скользило вниз под действием собственной силы тяжести, должно быть соблюдено условие α < φ.

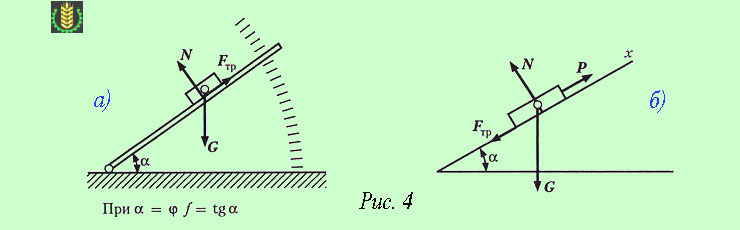
Наклонной плоскостью с переменным углом наклона к горизонту пользуются для экспериментального определения угла трения φ и коэффициента трения f (см. рисунок 4а).

Определим модуль силы Р, параллельной наклонной плоскости, в случае равномерного перемещения тела вверх по шероховатой наклонной плоскости (см. рисунок 4б). Спроецируем силы, действующие на тело, на ось x. Составим уравнение равновесия:

ΣX = 0; P – G sinα – F_тр = 0.

Так как F_тр = fG cosα, то P = G sinα + fG cosα или после преобразований: P = G (tgα + f).

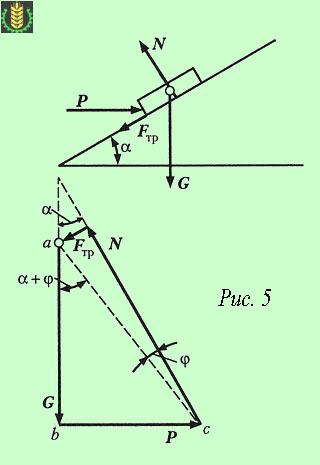
Определим модуль горизонтальной силы Р, которую надо приложить к телу для равномерного перемещения его вверх по шероховатой наклонной плоскости (см. рисунок 5).

Применим геометрическое условие равновесия плоской системы сил (размерами тела пренебрегаем) и построим замкнутый силовой многоугольник, соответствующий уравнению равновесия:

G + P + N + F_тр = 0.

Из треугольника abc имеем: P = Gtg(α + φ).

Этот случай движения имеет место при взаимном перемещении винта и гайки с прямоугольной резьбой, так как резьбу винта можно рассматривать как наклонную плоскость, угол наклона которой равен углу подъема винтовой линии.

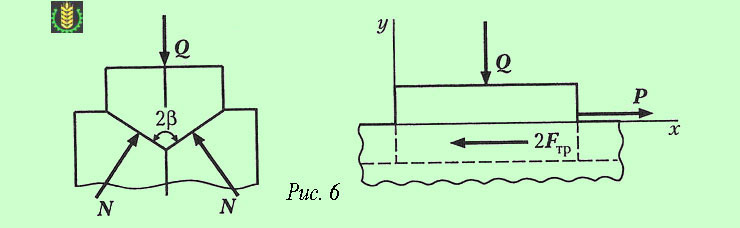
Трение в резьбе, имеющей треугольный или трапецеидальный профиль, подобно трению в клинчатом ползуне. Поэтому рассмотрим клинчатый ползун с углом заострения 2β, нагруженный вертикальной силой Q (см. рисунок 6). Определим силу P, необходимую для равномерного перемещения ползуна вдоль горизонтальных направляющих, если коэффициент трения скольжения равен f.

Составим два уравнения равновесия ползуна:

ΣX = 0; P – 2F_тр = 0; ΣY = 0; 2Nsinβ – Q = 0,

где F_тр – сила трения на каждой грани ползуна; N – нормальная реакция направляющей.

Решая эту систему уравнений и учитывая, что F_тр = fN, получим:

P = (f/sinβ)Q = f’Q,

где f’ = f/sinβ – приведенный коэффициент трения.

Соответствующий этому приведенному коэффициенту угол трения обозначим φ’ и назовем приведенным углом трения, тогда:

f’ = tgφ’.

Очевидно, что f’> f, следовательно, при прочих равных условиях трение в клинчатом ползуне больше трения на плоскости.

Понятие приведенного коэффициента трения условно, так как он изменяется в зависимости от угла заострения клинчатого ползуна.

По аналогии с движением тела вверх по наклонной плоскости под действием горизонтальной силы для равномерного перемещения клинчатого ползуна по направляющим, наклоненным к горизонту под углом α, нужно приложить горизонтальную силу равную

P = Q tg(α + φ’).

Трение в крепежной метрической резьбе подобно трению клинчатого ползуна с углом заострения 2β = 120˚, для трапецеидальной резьбы угол 2β = 150˚.

С трением связано понятие угла естественного откоса - наибольшим углом между наклонной плоскостью и горизонтом, при котором сыпучее тело удерживает свои частицы на поверхности, без их движения (осыпания) вниз. Угол естественного откоса сыпучего тела равен углу трения между его частицами. Этот угол приходится принимать во внимание, например, при различных земляных работах на уклонах и скатах.