Касательные напряжения и проверка прочности балок

по касательным напряжениям

Впроизвольной точке прямоугольного поперечного сечения балки (рис. 3.6) касательное напряжение определяют по формуле Д. И. Журавского:

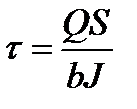(3.10)

где Q — поперечная сила в рассматриваемом сечении; статический момент относительно нейтральной оси z части площади сечения,

рис. 5. лежащей по одну сторону от уровня у, на котором опре­деляется напряжение; b—ширина сечения и J = bh³/12—момент инерции площади сечения относительно оси x.

Наибольшие касательные напряжения по­лучаются в точках нейтральной оси (у=0). Они имеют значение

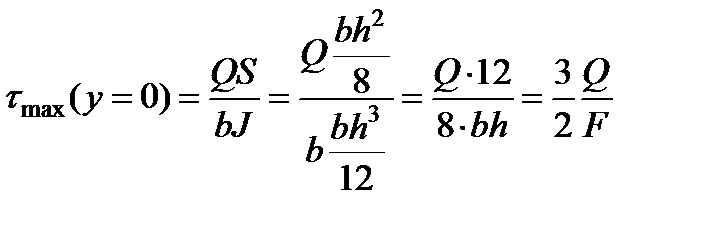(3.11)

где F=bh—площадь поперечного сечения балки.

По формуле (3.10) приближенно можно подсчитывать состав­ляющие касательных напряжений, перпендикулярные нейтральной оси, для балок непрямоугольного сечения, понимая под b ширину сечения на уровне рассматриваемой точки. Результирующие каса­тельные напряжения в точках контура сечения направлены по касательным к контуру сечения, а в других точках сечения они как-то наклонены к плоскости действия сил.

Точно найти касательные напряжений в балках произвольной формы сечения весьма сложно. Приближенное их определение ос­новано на некоторых произвольных допущениях о направлении касательных напряжений внутри сечения.

Прочность балки по касательным напряжениям проверяется в точках с максимальными касательными напряжениями того попе­речного сечения, в котором действует наибольшая по абсолютному значению поперечная сила Q_max.

Проверке следует подвергать короткие балки, балки с тонкой и высокой стенкой сечения, балки, изготовленные из материала, плохо сопротивляющего­ся сдвигу и балки, не­сущие

большие нагрузки вблизи опор. Провероч­ная формула имеет вид

где S_Q—статический мо­мент относительно нейт­ральной оси части попе­речного сечения, лежа­щей по одну сторону ли­нии действия т_тах; b_о— ширина сечения на ли­нии действия т_тах. Для большинства проверяемых сечений т_тах действует в точ­ках нейтральной оси.

Допускаемое касательное напряжение 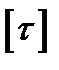обычно берут равным 0,5—0,7 от [ ]. Например, для СтОС и Ст2 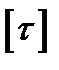= 90МПа, для Ст3 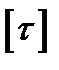= 100 МПа, для сосны и ели 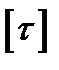=2МПа.

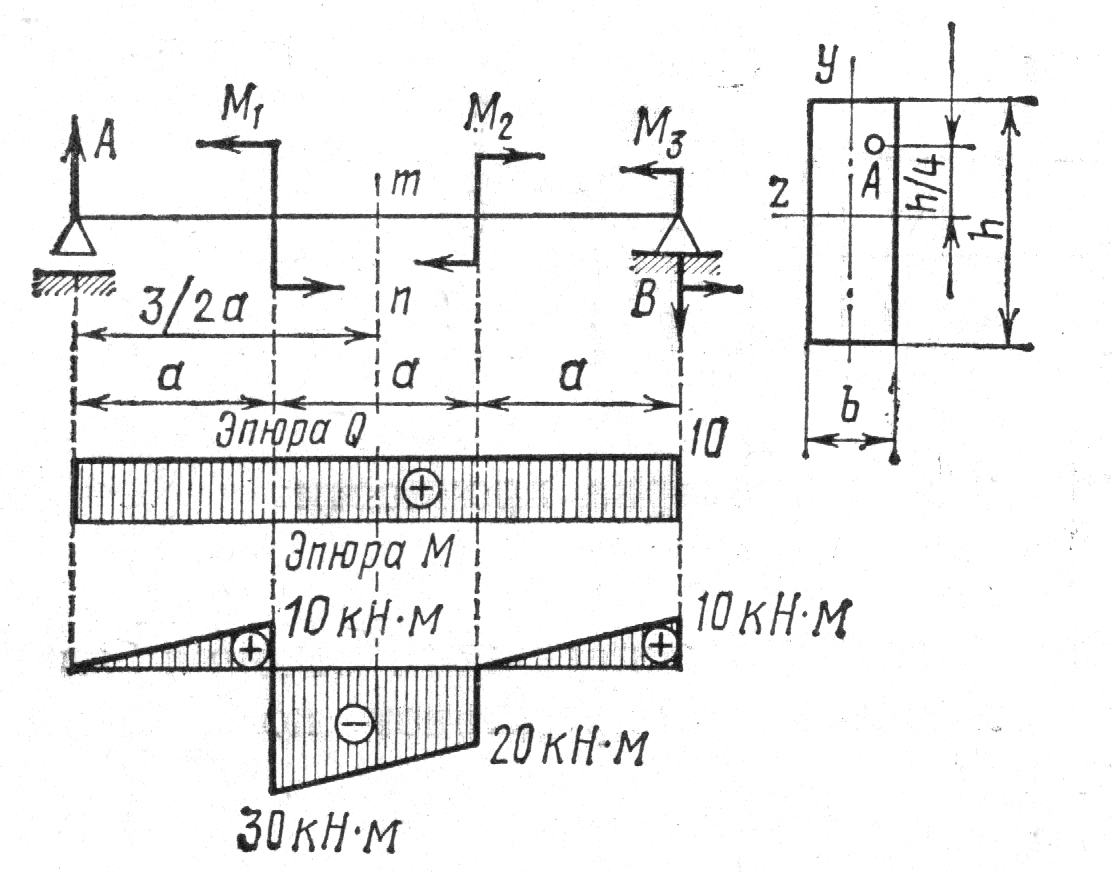Пример: Дано: М₁ = 40 кНм, М₂ = 20 кНм, М₃ = 10 кНм, а=1 м; 6 = 4 cm; h =12 см (рис. 6). Определить а_А и х_л в сечении

Решение. Реакции опор

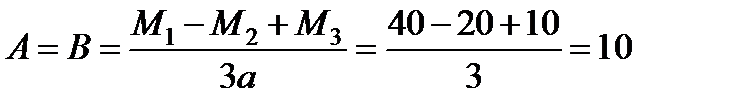кН.

Эпюры Q и М показаны на рис. 3.11. В сечении тп

М=- (30 + 20)/2 = - 25 кН-м; Q = 10 кН.

Так как точка А находится в растянутой зоне сечения, то по формуле (3.3) находим

Рис 6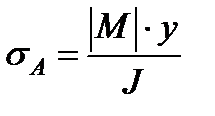

Для прямоугольного сечения

Для рассматриваемой точки А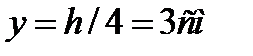

поэтому

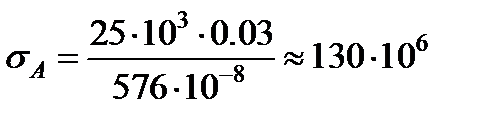Па = 130 МПа.

По формуле (3.10),