Расчет на контактную прочность

Расчет сводится к определению величины контактных напряжений, которые не должны превышать допустимых.

В качестве исходной принимают формулу Герца для наибольших контактных напряжений σ_н при сжатии 2-х цилиндров, соприкасающихся вдоль образующих:

,

где: q_n – нормальная к поверхности нагрузка на (см в кГс/см);

E_пр – приведенный модуль упругости материала:

,

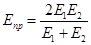если материалы шестерни и колеса равны, то

E_пр= E₁ = E₂;

ν – коэффициент поперечного сжатия (коэффициент Пуассона);

ρ_пр – приведенный радиус кривизны:

,
,
,

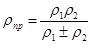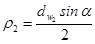ρ₁, ρ₂ – радиусы кривизны профилей шестерни и колеса.

Приведенная кривизна:

.

Подставим в формулу для σ_H значения q_n ρ_пр и E = 2,15 ×10⁶, после преобразований получим расчетную зависимость (в форме, рекомендованной по методике СЭВ)

,

где: z_H – коэффициент, учитывающий форму соприкасающихся поверхностей.

При α = 20˚, z_H = 1,77. В общем случае:

.

z_M – коэффициент, учитывающий механическое свойство материала:

.

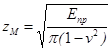Произведение z_H на z_M при α = 20˚ равно 1530.

z_ε – коэффициент, учитывающий влияние коэффициента торцового перекрытия:

.

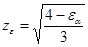При неточных расчетах можно принять z_ε = 0,9, что соответствует ε_α =1,6.

Подставляя:

,

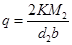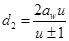
и числовые значения коэффициентов z_H, z_M, после преобразований получим:

.

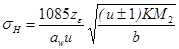При перспективности новой передачи задаются

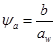
и по расчету определяют a_w:

.

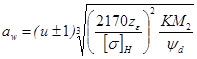Иногда необходимо или удобно определить диаметр шестерни “d₁”. Задаваясь

,

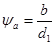после преобразования получим:

.

В случае расчета цилиндрических, косозубых или шевронных зубчатых колес во все формулы должны быть введены соответствующие поправки. Знак “+” относится к внешнему зацеплению, знак “–” к внутреннему.

14.2. Особенности расчета и конструкции
косозубых и шевронных зубчатых колес

Рис. 14.1. Схема сил, возникающих в косозубом зацеплении

Если прямозубые цилиндрические колеса применяют преимущественно при невысоких и средних окружных скоростях (5–20 м/с), в планетарных, открытых передачах, а также при необходимости осевого перемещения колес для переключения скоростей (коробки передач), то косозубые колеса применяют для ответственных передач, при средних и высоких скоростях (8–30 м/с). Объем использования косозубых колес составляет 30% от всех цилиндрических колес в машиностроении и непрерывно возрастает.

В отличие от прямозубых, косозубые передачи должны проектироваться так, чтобы в зацеплении находилось постоянно минимум две пары зубьев. Для этого необходимо, чтобы этого ширина колес (b) была больше осевого шага (t₀). При несоблюдении этого условия передача будет работать, как прямозубая.

При значительной ширине колеса и большом угле наклона зубьев в зацеплении может одновременно до десяти и больше пар зубьев. Зубья косозубых передач входят в зацепление постепенно: контакт начинается в точке по мере поворота колес контактная линия растет, некоторое время остается постоянной длины и далее постепенно сокращается до нуля. На боковых поверхностях зубьев контактные линии занимают наклонное положение.

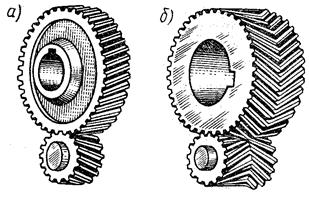
Рис. 14.2. Цилиндрические колеса:

а) косозубые; б) шевронные

В большинстве конструкций угол наклона зубьев “β ” принимают от 8˚ до 18˚ (редко до 25˚) с тем, чтобы обеспечить осевой коэффициент перекрытия в пределах не менее 1,1-1,2.

Точное значение угла “β ” выбирают таким, чтобы при стандартных значениях нормальных модулей межосевое расстояние “a_w” соответствовало стандартам.

Работа косозубой передачи связана с действием на опоры осевых нагрузок, поэтому в мощных редукторах применяют передачи, не передающие на опоры осевых нагрузок. Шевронные колеса представляют собой соединенные вместе два косозубых колеса с одинаковым, но противоположно направленным наклоном зубьев, и имеют угол наклона зубьев в пределах β = 25–40.

По форме расчета на прочность косозубых и шевронных колес аналогичен расчету цилиндрических колес, однако имеет свои особенности.

Расчеты на изгиб. Косые и шевронные зубья значительно (примерно на 30%) прочнее прямых ввиду того, что:

8) в зацеплении участвуют несколько пар зубьев , что учитывается коэффициентом К_α;

- контактная линия наклонена к основанию зуба, а сам зуб работает не как балка, а как пластина, что учитывается коэффициентом Y_β;

9) в опасном сечении зуб утолщен (другой коэффициент прочности зуба по местным напряжениям Y_K).

Коэффициент K принимают в зависимости от степени точности передачи (K_α > 1,0). При β ≤ 40 коэффициент 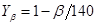(Y_β < 1,0) Коэффициент Y_F принимают в зависимости от эквивалентного числа зубьев Z_V по таблицам для цилиндрических прямозубых колес.

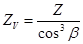
Эквивалентное число зубьев Z_V – это число зубьев эквивалентной прямозубой шестерни, имеющей радиус делительной окружности равный радиусу кривизны длительного цилиндра в сечении, нормальном к зубу. Если прочность на изгиб является основным критерием, то нормальный модуль определяется по формуле:

;

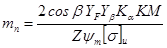где: .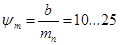

Если модуль определяется по заданному межосевому расстоянию (когда основным критерием является контактная прочность), то:

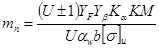
15. Общие сведения
о конических зубчатых передачах

Конические зубчатые колеса применяются в передачах между валами, оси которых расположены под углом. Основное применение имеют передачи с пересекающимися осями валов под углом 90˚. Передачи с межосевым углом, не равным 90˚, применяются редко. Из-за благоприятных условий компоновки в узлах машин, конические передачи широко применяются в машиностроении. Конические колеса выполняются с прямыми, косыми, круговыми и другими криволинейными зубьями. Прямозубые конические колеса рекомендуется применить при невысоких окружных скоростях (2-3 м/с). При более высоких скоростях – с круговыми зубьями, которые обеспечивают более плавное зацепление и большую несущую способность.

В конических передачах для обеспечения при сборке правильного контакта зубьев предусматривают возможность осевой регулировки зубчатых колес вместе с валами или относительно валов.