Личностно-ориентированного обучения
Поиск новых подходов и форм организации учебной работы с учащимися диктуется стремлением современной школы к развитию личности и интеллекта школьника в такой степени, чтобы выпускник школы был способен не только самостоятельно находить и усваивать ранее сгенерированную и обработанную информацию, но и сам мог генерировать новые идеи. Одним из направлений поиска решения этой проблемы является деятельностный подход к обучению и, в частности, использование в обучении метода проектов. Содержание и методика курса «Информатика и ИКТ» нацелены на формирование творческих и исследовательских качеств молодого человека. Для этого в руках педагога и ученика есть замечательный инструмент – компьютер. На уроках информатики школьник как настоящий исследователь наблюдает объекты и их поведение – информационные процессы, на основе наблюдений выдвигает гипотезу, проверяет её, используя компьютерную модель. Появляется исследовательское направление курса, в котором ключевым словом является творчество. Метод проектов в курсе информатики с успехом используется на трех этапах обучения: пропедевтическом, базовом, профильном. Значительная часть учебного времени (половина лабораторных работ) отводится работе школьников по системе индивидуальных и коллективных проектов. Такая форма работы позволяет учителю увидеть и использовать индивидуальные способности каждого школьника, и главное, используя новые современные информационные технологии обучения, привить детям вкус к творчеству и исследовательской деятельности.
Под учебным проектом понимается обоснованная, спланированная и осознанная деятельность обучаемого (обучаемых-партнеров), направленная на формирование у него (у них) определенной системы интеллектуальных и практических умений.
Целью метода проектов является развитие самообразовательной активности у учащихся. В результате творческой практической деятельности обучаемые создают конечный продукт в виде новых знаний и умений.
Метод проектов был разработан в начале XX века американским философом и педагогом Дж. Дьюи и его учеником В.Х. Килпатриком с целью ориентирования обучения на целенаправленную деятельность детей с учетом их личных интересов. В России идеи проектного обучения возникли практически параллельно с работами американских педагогов. Русский педагог С.Т. Шацкий в 1905 году организовал небольшую группу сотрудников, пытавшуюся активно использовать проектные методы в практике преподавания.
Сформулируем некоторые методические рекомендации для организации учебной деятельности учащихся в форме работы над проектом.
1. Учитель посвящает один урок беседе о проекте (системе проектов), подробно рассказывает о теме (темах) проектов, формулирует общую цель проекта, приводит примеры реализации некоторых подцелей. Встречные предложения учащихся приветствуются, а самостоятельно выдвинутая и обоснованная тема или конкретизированная цель проекта заслуживает особенного учительского внимания и поощрения.
2. Учащимся представляется достаточно широкий набор проектов (широкий набор возможностей реализации одного проекта) для реализации возможности реального выбора. Проекты могут быть как индивидуальными, так и коллективными.
3. Проект должен быть посильным для ученика. Работа над проектом мотивируется интересом обучаемого, а не только ответственностью.
4. Проект должен побуждать к получению новых знаний. Получение новых знаний правильно мотивируется, и этот мотив выставляет не преподаватель, а сам ученик.
5. Для организации работы над проектом, обучаемый может быть снабжен инструкцией по работе над проектом.
6. При работе над проектом ученику необходим консультант; в самом начале работы особенно важен индивидуальный контакт с преподавателем. Целесообразно для консультационной работы приглашать школьников-старшеклассников. Если у ученика нет опыта самостоятельной творческой работы, возможно «внедрение» преподавателя в исследовательскую группу детей на принципе равных интересов. Если ученик видит интерес преподавателя к работе, к конечному результату, он заражается от него этим интересом. Если при этом преподаватель откажется от поучений, а будет просто более опытным товарищем, которому интересен как проект, так и само общение, то достижение цели проекта гарантировано. Появляется уникальная возможность управлять работой учебной исследовательской группы изнутри.
7. При работе над проектом необходимо создавать условия, при которых школьники имеют возможность обсуждать друг с другом свои успехи и неудачи, при этом происходит взаимообучение.
8. Важна практическая значимость полученного результата работы над проектом и оценка этого результата со стороны окружающих, общественное признание результата. Получение результата – мотив работы над проектом. Учебный проект должен предполагать для исполнителя законченность и целостность проделанной им работы. Необходимо, чтобы завершенный проект был презентован и получил внимание взрослых и сверстников.
Этапы деятельности над проектом можно изобразить в виде схемы:
| Постановка проблемной ситуации | Þ | Формулирование целей | Þ | Создание проектных групп | Þ |
| Þ | Выбор тем, структурирование работы над проектом с указанием поэтапных результатов, обсуждение методов исследования | Þ | Работа над проектом | Þ | Оформление результатов и презентация проекта |
Задание. Разработайте проект по теме «Алгоритмизация и программирование». Вам дано одно задание по этой теме, необходимо расширить задание:
- обогатите проект познавательными, занимательными фактами по теме, желательно связанными с предложенным заданием;
- если возможно, предложите общий метод решения представленной задачи;
- разбейте задачу на подзадачи, решение которых приведет к решению главной задачи;
- усложните задачу, придумайте продолжение предложенной задачи;
- приведите примеры интересных познавательных задач и их решения по теме «Алгоритм и его свойства. Способы описания алгоритма»;
- разработайте и реализуйте презентацию Вашего проекта.
Проект 1. Суффиксная запись выражений
Некоторые понятия
Константы и переменные назовем операндами. При обычной записи выражений, называемой инфиксной, символы двуместной операции пишутся между операндами, k+m. В математике используется префиксная запись, при которой символы операций записываются перед операндами, sin(b), arccos(c). Здесь символы sin, arccos есть имена функций, они располагаются перед операндами. Можно рассматривать все операции, как имена функций, которые могут быть помещены до операндов или после них, так вместо x-y можно записать –; x; y или x; y ;–. Способы записи выражений, в которых символ двуместной операции стоит до или после операндов, а не разделяет их, предложены польским логиком Яном Лукасевичем (Jan Lukasiewiez) (1878-1957) и принято называть их польской префиксной или польской суффиксной записями соответственно.
Примеры суффиксной записи выражений. Так как в суффиксной записи имена двух переменных или констант могут стоять непосредственно одно за другим, то для их разделения применяется символ (;), назовем его разделителем.
| Обычная запись выражений | Суффиксная запись | Обычная запись выражений | Суффиксная запись |
| a/b k+l d*c | a;b;/ k;l;+ d;c;* | m-n
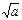 sin(a)
sin(a)
| m;n;-
a; 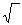 a;sin
a;sin
|
Вычисление значения выражения в суффиксной записи. Порядок выполнения операций в суффиксной записи определен порядком следования операндов и операций в выражении.
Алгоритм вычисления значения выражения можно описать так:
1. Просматриваем запись выражения слева направо.
2. Если встретится одноместная операция и предшествующий ей операнд, то применяем эту операцию к операнду и заменяем последовательность (операнд – операция) значением, т.е. операндом. Если встретится двуместная операция и предшествующие ей два операнда, то применяем операцию к операндам и заменяем последовательность (операнд – операнд – операция) значением, т.е. операндом и переходим к шагу 1; иначе значение выражения найдено, процесс вычисления закончен.
Например, вычислить значение выражения k;d;*;sin;b; 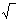 ;+ при заданных значениях переменных k, d, b можно так:
;+ при заданных значениях переменных k, d, b можно так:
1. Просматривая запись выражения слева направо, заменяем последовательность k;d;* значением выражения z2, равным k*d, последовательность b; 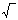 – значением выражения z1, равным
– значением выражения z1, равным 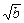 .
.
| k;d;* | ;sin; | b; 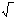
| ;+ |
| z2 | z1 |
Получим запись выражения z2;sin;z1;+.
2. Просматривая запись выражения, заменяем последовательность z2;sin значением z3, равным sin(z2).
| z2;sin; | z1;+ |
| z3 |
Получим запись выражения z3;z1;+.
3. Заменяем последовательность z3;z1;+ значением z4, равным z3+z1.
Пример. Вычислите значение выражения 5;3,1;2,9;+;-;3;“x2”;*.
Решение:
| 1. | 5; | 3,1;2,9;+ | ;-; | 3;“x2” | ;* |
| 6=3,1+2,9 | 9=32 |
| 2. | 5;6;- | ;9;* |
| -1=5-6 |
| 3. | -1;9;* |
| -9=-1*9 |
-9 – значение данного выражения.
Преобразование обычной записи выражений в суффиксную. Для преобразования обычной записи выражений в суффиксную запись изобразим выражение в виде бинарного дерева. Дерево – совокупность конечного числа узлов – вершин и попарно соединяющих эти вершины линий, называемых дугами или ребрами дерева. Первоначально выбранная вершина называется корнем дерева. Каждая операция соответствует вершине с меткой (символ операции). От вершины с символом операции исходят дуги, ведущие к операндам. В бинарном дереве каждый узел имеет самое большее два поддерева; в случае, когда имеется два поддерева, мы различаем левое и правое поддерево. Первый операнд двуместной операции мы изображаем в левом поддереве, второй операнд в правом поддереве.
Рассмотрим примеры представления выражения в виде бинарного дерева.
| Выражение | Дерево выражения | Выражение | Дерево выражения |
| a+b | 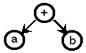
| n*m | 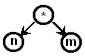
|
| n/c | 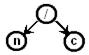
| tg(a) | 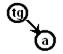
|
| k-m | 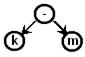
|
Пример. Изобразите выражение (c*d+k/l)/(n-m) в виде бинарного дерева.
Решение. Первая вершина дерева – корень, соответствует последней операции (делению) при вычислении значения этого выражения.
 Первый операнд (c*d+k/l) изобразим в левом поддереве. Второй операнд n-m – в правом поддереве.
Первый операнд (c*d+k/l) изобразим в левом поддереве. Второй операнд n-m – в правом поддереве.
Операнд (c*d+k/l) можно изобразить Операнд c*d – как дерево:
как бинарное дерево:

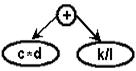
Операнд k/l – как дерево: Операнд n-m – как дерево:


Подставляя детализированные узлы, получаем дерево данного выражения:
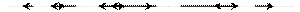
Для работы с древовидными структурами имеется множество алгоритмов с одной идеей – прохождением дерева. Это способ последовательного исследования узлов дерева, при котором каждый узел проходится точно один раз. Полное прохождение дерева дает линейное упорядочивание узлов. Для прохождения дерева используем концевой порядок прохождения: пройти левое поддерево, пройти правое поддерево, попасть в корень. При прохождении дерева выписываем символы в вершинах дерева, получаем линейную запись меток вершин – это и есть суффиксная запись выражения. В нашем примере это: c;d;*;k;l;/;+;n;m;-;/.
Обратная польская запись весьма полезна при вычислении выражений на компьютере.
Задание 1 к проекту 1. Напишите алгоритм для бездумного исполнителя преобразования записи обычного алгебраического выражения в обратную польскую (суффиксную) форму записи, т.е. A+(B-C)*D-F/(G+H) в форму записи – A;B;C;-;D;*;+;F;G;H;+;/;-.
Задание 2 к проекту 1.Задано уравнение вида f(x)=0, где выражение f(x) состоит из целых чисел, арифметических операций +,-,*,/ и переменной x, которая может входить в выражение не более одного раза. Выражение задаётся в обратной польской записи. Написать программу, которая решает заданное уравнение f(x)=0 и печатает все его корни. Длина исходной строки не превышает 80 символов. Элементы обратной польской записи разделяются пробелами.
Технические требования:
Программа должна обеспечивать следующий режим работы:
· печатает приглашение «>» и ожидает ввода строки;
· рассматривая введённую строку как обратную польскую запись выражения f(x), определяет и печатает все корни уравнения f(x) = 0, если корни отсутствуют, то печатает сообщение «корней нет».
Пример:
> 2 X * 4 - 7 / , ответ – уравнение имеет единственный корень 2.
Проект 2. Лабиринт. Попав в лабиринт, состоящий из одинаковых комнат, каждая из которых может иметь от 1 до 4 дверей в соседние комнаты, путник долго блуждая по нему, прошёл все имеющиеся в этом лабиринте двери (возможно не по одному разу), пока не нашел выход. На всякий случай путник составил описание своего маршрута, обозначая в каждой комнате направления движения соответственно буквами С (север), В (восток), Ю (юг), З (запад). Напишите алгоритм, который по заданному описанию маршрута путника определяет:
а) какой-нибудь другой допустимый путь;
б) какой-нибудь допустимый путь без захода дважды в одну и ту же комнату;
в) кратчайший из допустимых путей (длиной пути считается количество проходов через двери).
Проект 3. Тетраэдр. Одна из граней модели правильного тетраэдра красного цвета, остальные – синего. Модель поставили красной гранью на стол и стали «перекатывать» по его поверхности (перекатывая через ребро без скольжения). После нескольких таких переворачиваний модель вернулась на исходное место. Существует ли алгоритм «перекатывания» модели, пользуясь которым можно вернуть модель на исходное место так, чтобы она стояла на столе одной из синих граней. Если существует, то напишите этот алгоритм, если нет, то докажите это утверждение.
Проект 4. Максимальное значение. Дано целое десятичное число N (1£N£65535). Некто записал это число в двоичном формате и стал циклически сдвигать вправо, т.е. брать последнюю цифру числа и переносить ее в начало. Например, если N=11, то в двоичном формате оно будет представлено как 1011. После первого сдвига получится 1101, после второго – 1110, после третьего – 0111, после четвертого – исходное число 1011. Легко видеть, что максимальное значение из всех полученных таким образом чисел будет иметь число 1110, и это значение равно 14. Напишите алгоритм, который для заданного числа N определяет максимальное число из чисел, которые могут получаться в результате вышеописанных сдвигов.
Проект 5. Перестановки. Перестановкой из n различных элементов называется последовательность этих элементов, записанная, может быть, в другом порядке. Перестановки n чисел (1, 2, … , n) можно упорядочить, считая, что та из двух перестановок больше, у которой больше первый элемент. При одинаковых первых элементах больше та, у которой больше второй элемент и т.д. Например, перестановка (3, 5, 6, 1, 4, 2) больше, чем (3, 5, 4, 6, 2, 1). Перестановка (1, 2, 3, 4, 5, 6) – самая маленькая. Напишите алгоритм, определяющий по заданной перестановке, непосредственно следующую за ней, т.е. перестановку большую, чем заданная, но меньшую, чем любая другая, большая, чем заданная. Входные данные: число n – количество чисел в перестановке и последовательность из n чисел, образующих эту перестановку.
Проект 6. Квадрат палиндрома. Число называется палиндромом, если его запись читается одинаково с начала и с конца. Напишите алгоритм нахождения всех шестизначных палиндромов, квадраты которых также являются палиндромами. Из числовых типов разрешается использовать только тип Integer.
Проект 7. Латинские квадраты. Матрица A называется латинским квадратом порядка N, если каждое из чисел 1, 2, … , N входит ровно один раз в каждую строку и в каждый столбец матрицы A. Напишите алгоритм вычисления количества различных латинских квадратов с фиксированной первой строкой 1, 2, … , N для 1<N<7.
Из истории латинских квадратов
Считается, что название «латинский квадрат» для обозначения описанной матрицы связано с тем, что Леонард Эйлер около 1780 г. использовал латинские буквы для обозначения символов внутри квадрата. Заинтересовавшись старой математической головоломкой, он установил существование пар ортогональных латинских квадратов любого порядка, не имеющего вид 4n+2, но, несмотря на длительные поиски, не смог найти ни одной пары шестого порядка. В конце концов, он предположил, что не существует пар латинских квадратов шестого порядка и любого порядка вида 4n+2.
Гипотеза Эйлера продержалась столетия; для шестого порядка она была доказана только в начале двадцатого века путем исчерпывающего перебора всех вариантов, что без применения ЭВМ представляет собой задачу необычайной трудности. Когда стали доступны ЭВМ, их можно было бы использовать для решения задачи десятого порядка, но в данном случае они появились на сцене слишком поздно, так как в 1959 г. гипотеза была, наконец, опровергнута за счет общего построения, приводящего (без ЭВМ) к ортогональным латинским квадратам любого порядка 4n+2³10. Впоследствии были составлены сравнительно быстрые (учитывая сложность этой комбинаторной задачи) программы для нахождения многих пар десятого порядка.
Многие задачи, связанные с очередностью событий, составлением расписания, распределением заданий или ресурсов при их идеализации (чтобы задача стала более простой) можно сформулировать при помощи латинских квадратов. Приведем пример такой задачи. В школе четыре преподавателя Т1, Т2, Т3, Т4 в течение дня проводят занятия с четырьмя классами С1, С2, С3, С4. Каждый преподаватель должен дать урок в каждом классе один раз в течение дня. Написать возможные варианты составления расписания на один день.
| А= | С1 | С2 | С3 | С4 | Возможное расписание можно изобразить матрицей A, число K в строке i и столбце j означает, что преподаватель Ti занимается в классе Cj во время K. Легко видеть, что данное расписание – латинский квадрат, так как один преподаватель не может одновре- | |
| Т1 | ||||||
| Т2 | ||||||
| Т3 | ||||||
| Т4 |
менно заниматься с двумя классами и никакое целое число (час) не может встретиться дважды в одной строке; так как два преподавателя не могут одновременно заниматься с одним и тем же классом. Никакое целое число (час) не встречается дважды в одном столбце.
Проект 8. Ортогональные латинские квадраты. Матрица А размером N´N назовем латинским квадратом (см. Проект 7) порядка N, если каждое из чисел 1, 2, … , N входит ровно один раз в каждую строку и в каждый столбец этой матрицы. Латинские квадраты А и В назовем ортогональными, если при их наложении в новой матрице получается множество всех упорядоченных пар элементов (среди N пар соответствующих компонентов нет двух одинаковых). Например, для ниже приведенных латинских квадратов А и В матрица С определяет их ортогональность.
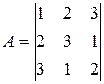 ,
, 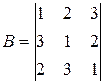 ,
, 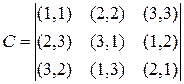
Напишите алгоритм, в результате исполнения которого будут получены по одной паре ортогональных латинских квадратов для всех значений N от 2 до 9 в формате матрицы C.
Проект 9. Уникурсальная линия. Линия называется уникурсальной, если её можно начертить, не отрывая карандаша от бумаги и не проходя два раза одно и то же звено. Линии, содержащей N узлов, можно сопоставить квадратную матрицу порядка N – матрицу смежности, элемент a(i,j), которой равен 1, если узел i соединен с узлом j некоторым отрезком, не содержащим других узлов, и 0 в противном случае (i, j=1, 2, … , N). Для линии, изображенной на рисунке, матрица смежности имеет вид:

|
|
Дана матрица соединений с N узлами. Напишите алгоритм, определяющий является ли линия, заданная матрицей смежности, уникурсальной, если да, то алгоритм должен находить хотя бы одну последовательность номеров узлов, которые образуют требуемый путь.
Замечание. Узлы А и В смежные, если существует отрезок, соединяющий узел А с узлом В. Линия называется связной, если все ее узлы связаны. Известно, что линия уникурсальна тогда и только тогда, когда она связна и число тех ее узлов, из которых выходит нечетное число звеньев, не больше двух.
Проект 10. Транспортная сеть.В городе имеется M площадей и K дорог, соединяющих эти площади. Каждая дорога соединяет две площади, длина каждой дороги равна 1.
Задания.
1. Требуется спланировать одностороннее движение по дорогам так, чтобы с любой площади можно было бы проехать до любой другой.
2. Решить задачу так, чтобы максимальное время движения между двумя площадями было минимальным.
| Образец ввода: Введите количество площадей: M Введите количество дорог K Дорогой 1 связаны площади: ………………………………….. Дорогой k связаны площади: ………………………………… | Замечание. При выводе результата для каждой дороги указать площади в порядке, соответствующем направлению спланированного движения. Для второй задачи необходимо указать максимальное время движения между парами площадей, если время движения между двумя любыми площадями, соединёнными дорогой, равно 1. Количество площадей не превосходит 50. |
Проект 11. Переправа. На берегу реки находятся: лодочник, волк, коза и капуста. У берега реки расположена лодка. Лодочник должен переправить волка, козу и капусту на другой берег реки. При перевозке в лодке с лодочником может находиться либо только волк, либо только коза, либо только капуста. Если оставить волка с козой или козу с капустой без лодочника, то волк съест козу или коза съест капусту. Разработать программу игрового характера, моделирующую действия лодочника.
| Технические требования | |
| Программа должна изображать начальное состояние переправы, реализовывать управление выбором переправляющихся, изображать состояние переправы в результате этого выбора. | В программе так же нужно реализовать управление ходом переправы, перемещение переправляющихся и изображение состояния переправы после каждого такта перемещения. |
Дата добавления: 2015-01-26; просмотров: 1190;
