Пирамидальной сортировки элементов массива
Задача 1. Разработайте алгоритм пирамидальной сортировки линейного массива и напишите программу на языке Turbo Pascal.
Решение
Алгоритм пирамидальной сортировки разработан Дж. Уильямсом и Р.У. Флойдом. Это улучшенный метод сортировки, основанный на принципе выбора. Методы сортировок используют многократные просмотры массивов и их частей и выполнение определенных операций над их элементами. Метод сортировки простым выбором базируется на повторном выборе наибольшего (наименьшего) элемента из n элементов, затем выбора наибольшего (наименьшего) элемента из n-1 элемента и т.д. Для улучшения метода сортировки простым выбором необходимо получать от каждого прохода больше информации, чем указание на один наибольший (наименьший) элемент. Алгоритм пирамидальной сортировки использует при выборе наибольшего (наименьшего) элемента представление сортируемого массива в виде нелинейной структуры – специального двоичного (бинарного) дерева (пирамиды).
Некоторые определения
Графом G называют пару множеств (W,E), где W – это непустое конечное множество элементов, которое мы назовем вершинами графа, а E – это конечное множество неупорядоченных или упорядоченных пар элементов множества W. Элементы множества E – ребра или дуги. Неупорядоченную пару вершин {V, U} будем называть ребром, а упорядоченную пару назовем дугой <V, U> (V – начало дуги, U – конец дуги). Две вершины U и V графа G называются смежными, если существует соединяющее их ребро {U, V}. При этом вершины U и V называются инцидентными этому ребру, а ребро инцидентным этим вершинам. Два ребра называются смежными, если они имеют, по крайней мере, одну общую вершину. Цепью в графе называется чередующаяся последовательность вершин и ребер: V0, l1, V1, l2 ,V2 , … , lk, Vk, в которой любые два соседних элемента инцидентны и все ребра различны. Если V0=Vk, то цепь называется циклом. Если все вершины в цепи различны, то цепь называется простой. Если в графе любые две вершины соединены цепью, то граф называется связным. Деревом называется связный граф без циклов. При изображении графов на рисунках рёбра и дуги изображаются линиями, у дуг на концах изображаются стрелки, указывающие направление связи вершин, вершины – точками, окружностями или квадратами. Такое представление графа называется диаграммой. Диаграмма графа, это информационная модель объекта, это информация о составе и структуре системы, представленная в графической форме. Отношения между вершинами дерева определяются в терминах взятых из генеалогической терминологии. Вершина A, которая находится над другой вершиной C и непосредственно соединена с ней ребром, называется предком вершины C. Если вершина A является предком вершины C, то вершина C называется потомком вершины A. Корень дерева – это вершина, не имеющая предков (первоначально выбранная вершина). Листья дерева – это вершины, не имеющие потомков. Вершина со своими потомками называется поддеревом основного дерева. Бинарным деревом называется дерево, в котором каждая вершина имеет не более двух потомков. В случае, когда вершина имеет два потомка, принято различать левого и правого потомка.
Возьмем массив Mass = (14, 5, 23, 57, 4, 31, 11, 18, 70, 42, 3, 9) и поставим в соответствие этому массиву бинарное дерево B. Каждому элементу массива поставим в соответствие вершину бинарного дерева, а отношения между элементами массива установим ребрами.

| Уровень | Узлы 2, 3 4, 5, 6, 7 8, 9, 10, 11, 12 |
Натуральными числами начиная с 1 и далее «сверху вниз» по уровням и «слева направо» на одном уровне пронумеруем все вершины бинарного дерева B, а следовательно и все соответствующие элементы массива. Эти номера (адреса) поставлены около вершин. Корень дерева имеет адрес 1, содержимое корня – 14. Рассмотрим вершину с адресом 2, содержимое этой вершины – 5. Она имеет предка – вершину с адресом 1 и двух потомков – вершины с адресами 4 и 5. Вершина с адресом 6 имеет предка – вершину с адресом 3 и одного потомка – вершину с адресом 12. Вершина с адресом 7 имеет предка с адресом 3 и не имеет потомков. Вершины с адресами 8, 9, 10, 11, 12, 7 – листья (они не имеют потомков). Адреса предков и потомков вершины с адресом k можно вычислить по формулам:
- для предков pred(k) = k\2, где k = 1,2,…,n;
- для потомка слева left(k) = 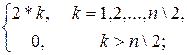
- для потомка справа right(k) = 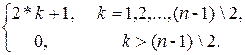 .
.
Введем понятие пирамиды. Пусть дан массив Mass:
Mass(1), Mass(2), … , Mass(n). (1)
Пирамидой называется непустая последовательность элементов массива (1):
Mass(p), Mass(p+1), … , Mass(q), где 1£p£q£n,
для которой выполнено одно из следующих условий:
1) 2p>q;
2) 2p = q и Mass(p)³Mass(q);
3) 2p£q и Mass(j)³Mass(2j), для p£j£q/2,
Mass(j)³Mass(2j+1), для p£j£(q-1)/2.
Следствия:
1) для любой последовательности (1) подпоследовательность
Mass(n\2+1), Mass(n\2+2), … , Mass(n)
является пирамидой;
2) если последовательность (1) – пирамида, то
 ;
;
3) если последовательность (1) – пирамида и представлена в виде бинарного дерева B, то значение любого узла в B будет не меньше значений его левого и правого потомков.
| Пирамида, составленная из элементов массива Mass=(14, 5, 23, 57, 4, 31, 11, 18, 70, 42, 3, 9) – это последовательность (70, 57, 31, 18, 42, 23, 11, 14, 5, 4, 3, 9). Двоичное дерево, соответствующее пирамиде представлено на рисунке. | 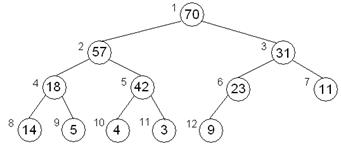
|
Алгоритм пирамидальной сортировки
алг пирамидальная_сортировка (аргцел n, аргрезвещтаб Mass[1:n])
дано || массив вещественных чисел Mass[1:n]
надо || отсортированный по возрастанию массив Mass
нач
│1 шаг. Выбери наибольший элемент из n элементов массива Mass
│путем построения пирамиды из n элементов.
│2 шаг. Поменяй местами первый и последний элементы массива
│Mass, поставив наибольший из n элементов на последнее место в
│массиве.
│3 шаг. Выбери наибольший из первых n-1 элементов массива Mass
│путем построения из них пирамиды.
│4 шаг. Поменяй местами первый и последний элементы просмат-
│риваемой части массива Mass, поставив наибольший элемент из
│первых n-1 элементов на n-1 место в массиве Mass.
│5 шаг. Выбери наибольший из первых n-2 элементов массива Mass
│путем построения из них пирамиды.
│6 шаг. Поменяй местами первый и последний элементы просмат-
│риваемой части массива Mass, поставив наибольший элемент из
│первых n-2 элементов на n-2 место в массиве Mass.
│и т.д.
кон
Итак, шаги 2 и 3 повторяются n-1 раз для последовательно укорачивающегося справа на 1 элемент массива Mass. Реализация шага 1 отличается от реализации шагов 3, 5, 7 и т.д. На шаге 1 наибольший элемент выбирается путем построения пирамиды из всех элементов массива Mass: первоначально пирамида строится на основании следствия 1, далее последовательно к выбранной или построенной пирамиде добавляется слева элемент массива Mass(k), и при помощи просеивания добавленный элемент помещается на соответствующее место, чтобы снова получилась пирамида. Элементы добавляются и просеиваются, начиная с элемента Mass(n\2) до Mass(1).
Алгоритм пирамидальной сортировки можно переписать так:
алг пирамидальная_сортировка (аргцел n, аргрезвещ таб Mass[1:n])
дано || массив вещественных чисел Mass[1:n]
надо || отсортированный по возрастанию массив Mass
нач
│Построй пирамиду из n элементов массива Mass.
│нц Повтори n-1 раз
││1. Поменяй местами первый и последний элементы построенной
││пирамиды из элементов массива Mass, и укороти для исследования
││просматриваемую часть массива справа на 1 элемент.
││2. Построй пирамиду из исследуемой части массива Mass путем
││просеивания только 1-го элемента.
│ кц
кон
Детализируем 1 шаг алгоритма – построение пирамиды из n элементов массива Mass. Выберем из заданного массива (1) последовательность, которая заведомо является пирамидой. По следствию 1 это последовательность:
Mass(n\2+1), Mass(n\2+2), … , Mass(n), (2)
т.к. выполнено условие 2*(n\2+1)³n или 2p>q, где p = n\2+1 и q = n. Элементы последовательности (2) на бинарном дереве соответствуют листьям. Расширим пирамиду влево, добавляя к ней слева по одному оставшемуся элементу из массива (1) и, просеивая этот элемент по потомкам, поместим его на соответствующее место в наращенной пирамиде. Добавим к пирамиде (2) элемент Mass(n\2) и обозначим n\2 через i. Будем иметь
Mass(i), Mass(i+1), … , Mass(n). (3)
Преобразуем (3) в пирамиду. Для этого сравним Mass(i) с его потомками Mass(2*i) и Mass(2*i+1). Если Mass(i) не меньше своих потомков, то просеивание элемента Mass(i) заканчиваем, т.к. (3) – пирамида, в противном случае обмениваем значения Mass(i) и max(Mass(2*i),Mass(2*i+1)). Опустившийся элемент в последовательности (3) продолжаем просеивать тем же способом, пока последовательность (3) не станем пирамидой (смотри иллюстрацию исполнения пирамидальной сортировки для конкретного массива). Продолжая наращивать пирамиду (3), преобразуем весь массив (1) в пирамиду. Назовем пирамиду текущей.
Детализируем шаг 2, который состоит из 2-х шагов: 2.1 и 2.2.
Шаг 2.1. В полученной пирамиде Mass первый элемент не меньше остальных, поставим его на последнее (свое) место, а последний элемент текущей пирамиды – на первое. Укоротим рассматриваемую часть массива на один элемент справа.
Шаг 2.2. Рассмотрим укороченную справа последовательность элементов, она уже может и не быть пирамидой. Для построения пирамиды необходимо просеять один первый элемент.
Далее шаги 2.1 и 2.2 повторить n-2 раза. В результате получим отсортированный по возрастанию массив.
Program HeapSort;
Uses Crt;
Const byteN=12;
Var byteI,byteK:byte; massA:real; Mass:array [1..byteN] of real;
Procedure Sift (byteX,byteK:byte);
Var byteY:byte;
Begin
byteY:=2*byteX; {Нахождение индексов потомков элемента Мass[byteX]}
While byteY<=byteK do {Организация просеивания элемента Mass[byteX] по бинарному дереву для построения пирамиды}
begin
If byteY<byteK then
{Выбор большего элемента последовательности из потомков (Mass[byteY] и Mass[byteY]) элемента Mass[byteX]}
If Mass[byteY]<Mass[byteY+1] then
byteY:=byteY+1;
{Выбор большего элемента из элемента Mass[byteX] и его потомков; если элемент Mass[byteX] больше своих потомков, то дерево построено и
просеивание закончено, иначе переставляются элементы Mass[byteX] и
max(Mass[byteY],Mass[byteY+1]) и просеивание продолжается}
If Mass[byteY]<=Mass[byteX] then break;
massA:=Mass[byteX]; Mass[byteX]:=Mass[byteY];
Mass[byteY]:=massA; byteX:=byteY; byteY:=2*byteX
end;
End;
BEGIN
For byteI:=1 to byteN do {Ввод элементов сортируемого массива}
begin
Write('Mass[',byteI,']='); ReadLn(Mass[byteI])
end;
{Построение пирамиды из последовательности чисел}
byteI:=(byteN div 2)+1; {Вычисление индекса первого элемента
последовательности для просеивания}
While byteI>1 do
begin
byteI:=byteI-1; Sift(byteI,byteN);
end;
byteK:=byteN;
While byteK>1 do
begin
massA:=Mass[1]; {Перестановка первого и последнего элементов}
Mass[1]:=Mass[byteK]; {исследуемой последовательности}
mass[byteK]:=massA;
byteK:=byteK-1; {Нахождение индекса последнего элемента укороченной последовательности}
Sift(1,byteK) {Просеивание первого элемента последовательности}
end;
For byteI:=1 to byteN do
Write(Mass[byteI]:6:2)
END.
Иллюстрация исполнения пирамидальной сортировки для
конкретного массива
Дано:
| Индексы | ||||||||||||
| Значения | ||||||||||||
| Таблица значений и индексов элементов массива Mass |

Решение
1 шаг

| Последовательность 11,18,70,42, 3, 9 – пирамида 7 8 9 10 11 12 | |||
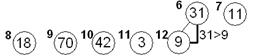
| Наращиваем пирамиду слева элементом 31 и просеиваем этот элемент по его потомкам: 31,11,18,70,42, 3, 9
 6 7 8 9 10 11 12
Т.к. 31>9, оставляем 31 на своем месте. Полученная последовательность – пирамида. 6 7 8 9 10 11 12
Т.к. 31>9, оставляем 31 на своем месте. Полученная последовательность – пирамида.
| |||
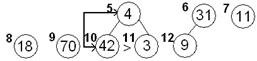
| Наращиваем пирамиду слева элементом 4 и просеиваем этот элемент по его потомкам
4,31,11,18,70,42, 3, 9
 5 6 7 8 9 10 11 12
42>3 5 6 7 8 9 10 11 12
42>3
| |||
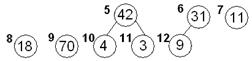
| Меняем местами элементы 4 и 42 42,31,11,18,70, 4, 3, 9 5 6 7 8 9 10 11 12 У элемента 4 потомков нет, просеивание закончено, полученная последовательность – пирамида. | |||
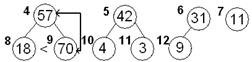
| Наращиваем пирамиду слева элементом 57 и просеиваем этот элемент по его потомкам
57,42,31,11,18,70, 4, 3, 9
 4 5 6 7 8 9 10 11 12
18<70 4 5 6 7 8 9 10 11 12
18<70
| |||
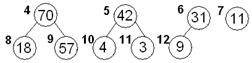
| Меняем местами элементы 57 и 70 70,42,31,11,18,57, 4, 3, 9 4 5 6 7 8 9 10 11 12 У элемента 57 потомков нет, просеивание закончено, полученная последовательность – пирамида. | |||
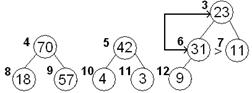
| Наращиваем пирамиду слева элементом 23 и просеиваем этот элемент по его потомкам
23,70,42,31,11,18,57, 4, 3, 9
 3 4 5 6 7 8 9 10 11 12
31>11 3 4 5 6 7 8 9 10 11 12
31>11
| |||

| Меняем местами элементы 23 и 31
31,70,42,23,11,18,57, 4, 3, 9
 3 4 5 6 7 8 9 10 11 12
Т.к. 23>9, оставляем 23 на своем месте. Полученная последовательность – пирамида. 3 4 5 6 7 8 9 10 11 12
Т.к. 23>9, оставляем 23 на своем месте. Полученная последовательность – пирамида.
| |||
 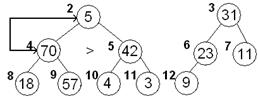
| Наращиваем пирамиду слева элементом 5 и просеиваем этот элемент по его потомкам 5,31,70,42,23,11,18,57, 4, 3, 9 2 3 4 5 6 7 8 9 10 11 12 70>42 | |||
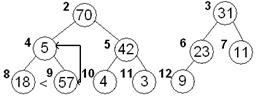
| Меняем местами элементы 5 и 70 и просеиваем далее элемент 5 по его потомкам
70,31,5,42,23,11,18,57, 4, 3, 9
2 3 4 5 6 7 8 9 10 11 12
 18<57
18<57
| |||
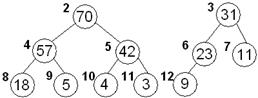
| Меняем местами элементы 5 и 57 70,31,57,42,23,11,18, 5, 4, 3, 9 2 3 4 5 6 7 8 9 10 11 12 У элемента 5 потомков нет, просеивание закончено, полученная последовательность – пирамида. | |||
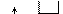 
| Наращиваем пирамиду слева элементом 14 и просеиваем этот элемент по его потомкам 14,70,31,57,42,23,11,18, 5, 4, 3, 9 1 2 3 4 5 6 7 8 9 10 11 12 70>31 | |||
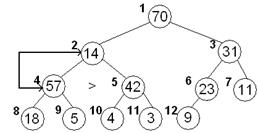
| Меняем местами элементы 14 и 70 и просеиваем далее элемент 14 по его потомкам
70,14,31,57,42,23,11,18, 5, 4, 3, 9
 1 2 3 4 5 6 7 8 9 10 11 12
57>42 1 2 3 4 5 6 7 8 9 10 11 12
57>42
| |||
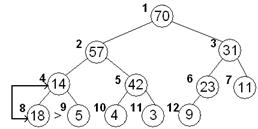
| Меняем местами элементы 14 и 57 и просеиваем далее элемент 14 по его потомкам
70,57,31,14,42,23,11,18, 5, 4, 3, 9
 1 2 3 4 5 6 7 8 9 10 11 12
18>5 1 2 3 4 5 6 7 8 9 10 11 12
18>5
| |||
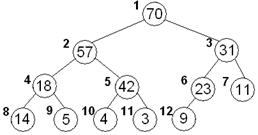
| Меняем местами элементы 14 и 18 70,57,31,18,42,23,11,14, 5, 4, 3, 9 1 2 3 4 5 6 7 8 9 10 11 12 У элемента 14 потомков нет, просеивание закончено, полученная последовательность – пирамида. | |||
Выполнение шага 1 закончено, построенная последовательность, содержащая все элементы массива Mass, пирамида.

 2 шаг
2 шаг
2.1. Mass=(70,57,31,18,42,23,11,14,5,4,3,9). Меняем местами в пирамиде первый и последний элементы 9,57,31,18,42,23,11,14, 5, 4, 3,70
1 2 3 4 5 6 7 8 9 10 11 12
Усекаем справа последовательность на 1 элемент (он стоит на своем месте)
9,57,31,18,42,23,11,14, 5, 4, 3 || 70
1 2 3 4 5 6 7 8 9 10 11
2.2. Просеиваем элемент Mass(1)=9 по своим потомкам
9,57,31,18,42,23,11,14, 5, 4, 3
 1 2 3 4 5 6 7 8 9 10 11
1 2 3 4 5 6 7 8 9 10 11
57>31
_____________________________________________________________________________________________________
57, 9,31,18,42,23,11,14, 5, 4, 3
 1 2 3 4 5 6 7 8 9 10 11
1 2 3 4 5 6 7 8 9 10 11
18<42
|
_____________________________________________________________________________________________________
57,42,31,18, 9,23,11,14, 5, 4, 3
 1 2 3 4 5 6 7 8 9 10 11
1 2 3 4 5 6 7 8 9 10 11
4>3
2.1 Полученная последовательность (57,42,31,18,9,23,11,14,5,4,3) – пирамида. Меняем местами первый и последний элементы последовательности и усекаем справа последовательность на один элемент (он стоит на своем месте в получаемом массиве)
3,42,31,18, 9,23,11,14, 5, 4 || 57
1 2 3 4 5 6 7 8 9 10
2.2 Просеиваем элемент Mass(1)=3 по его потомкам и получаем пирамиду
42,18,31,14,9,23,11,3,5,4
| Шаги | Элементы рассматриваемой последовательности | Массив Mass |
| 2.1 | 4,18,31,14,9,23,11,3,5 || 42 | (4,18,31,14,9,23,11,3,5,||42,57,70) |
| 2.2 | 31,18,23,14,9,4,11,3,5 | (31,18,23,14,9,4,11,3,5,||42,57,70) |
| 2.1 | 5,18,23,14,9,4,11,3 || 31 | (5,18,23,14,9,4,11,3,||31,42,57,70) |
| 2.2 | 23,18,11,14,9,4,5,3 | (23,18,11,14,9,4,5,3,||31,42,57,70) |
| 2.1 | 3,18,11,14,9,4,5 || 23 | (3,18,11,14,9,4,5,||23,31,42,57,70) |
| 2.2 | 18,14,11,3,9,4,5 | (18,14,11,3,9,4,5,||23,31,42,57,70) |
| 2.1 | 5,14,11,3,9,4 || 18 | (5,14,11,3,9,4,||18,23,31,42,57,70) |
| 2.2 | 14,9,11,3,5,4 | (14,9,11,3,5,4,||18,23,31,42,57,70) |
| 2.1 | 4,9,11,3,5 || 14 | (4,9,11,3,5,||14,18,23,31,42,57,70) |
| 2.2 | 11,9,4,3,5 | (11,9,4,3,5,||14,18,23,31,42,57,70) |
| 2.1 | 5,9,4,3 || 11 | (5,9,4,3,||11,14,18,23,31,42,57,70) |
| 2.2 | 9,5,4,3 | (9,5,4,3,||11,14,18,23,31,42,57,70) |
| 2.1 | 3,5,4 || 9 | (3,5,4,||9,11,14,18,23,31,42,57,70) |
| 2.2 | 5,3,4 | (5,3,4,||9,11,14,18,23,31,42,57,70) |
| 2.1 | 4,3 || 5 | (4,3,||5,9,11,14,18,23,31,42,57,70) |
| 2.2 | 4,3 | (4,3,||5,9,11,14,18,23,31,42,57,70) |
| 2.1 2.2 | 3 || 4 | (3,||4,5,9,11,14,18,23,31,42,57,70) (3,4,5,9,11,14,18,23,31,42,57,70) |
Сортировка закончена. Отсортированный массив имеет вид:
Mass=(3,4,5,9,11,14,18,23,31,42,57,70)
Выбор наибольшего из (n-1) элемента массива, из (n-2) элементов массива и т.д. упрощается за счет получения большей информации при нахождении наибольшего из n элементов массива. Для больших n пирамидальная сортировка оказывается очень эффективной, она требует 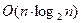 шагов, где n – число элементов массива.
шагов, где n – число элементов массива.
Дата добавления: 2015-01-26; просмотров: 2250;
