Основы теории подобия центробежных насосов
Обобщение экспериментальных данных, полученных при испытании модели, и использование их при проектировании натурных насосов возможно лишь при соблюдении определенных правил, устанавливаемых в теории подобия.
Явления называют подобными, если по известным характеристикам одного из них можно получить характеристики другого простым пересчетом. При этом в подобных системах должны наблюдаться процессы одинаковой физической природы.
Для полного подобия насосов должно выполняться их геометрическое, кинематическое и динамическое подобие. Системы называются геометрически подобными, если все соответственные их линейные размеры пропорциональны, а углы равны. При соблюдении геометрического подобия натурного и модельного насосов, кинематическое подобие определяет подобие планов скоростей, т.е.
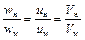 ,
,
где индекс "н" обозначает натурный насос, а "м" – модельный.
Для динамического подобия (подобия сил) требуется равенство критериев Рейнольдса у натуры и модели. Критерий Рейнольдса для насоса определяют по формуле
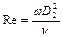 ,
,
гдеw – угловая скорость рабочего колеса;D2 – его наружный диаметр.
Опыт показывает, что в большинстве случаев насосы работают в области автомодельности, т.е. в области, в которой характеристики насоса не зависят от критерия Рейнольдса. Эта область наблюдается при Re>1000.
Обозначим отношение линейных размеров натурного и модельного насосов 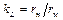 . Принимая во внимание, что угловая скорость связана с частотой вращения рабочего колеса следующим соотношением
. Принимая во внимание, что угловая скорость связана с частотой вращения рабочего колеса следующим соотношением 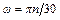 , из условия кинематического подобия получим
, из условия кинематического подобия получим
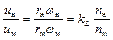 .
.
Подобие подач. Подача насоса связана с геометрическими и кинематическими характеристиками рабочего колеса уравнением (3.7)
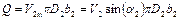 .
.
Отношение подач натурного и модельного насосов
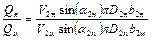 .
.
Поскольку у подобных насосов планы скоростей подобны, то 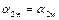 . Кроме того, наличие геометрического и кинематического подобия позволяют записать следующие равенства:
. Кроме того, наличие геометрического и кинематического подобия позволяют записать следующие равенства:
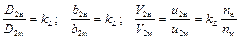 .
.
Следовательно,
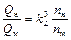 ,
,
т.е. у подобных насосов отношение подач пропорционально произведению соотношения линейных размеров в третьей степени на соотношение частот вращения рабочих колес.
Подобие напоров. Ранее были получены уравнения для определения теоретического и действительного напоров:
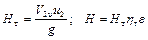 .
.
Полагая, что гидравлические КПД hг и коэффициенты, учитывающие конечное число лопаток e у модели и натуры одинаковы, получим
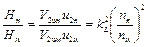 ,
,
что отношение напоров у подобных насосов пропорционально произведению квадратов соотношений линейных размеров и частот вращения рабочих колес.
Подобие мощностей. Мощность насоса определяют по формуле
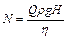 .
.
При работе натурного и модельного насосов на одной и той же жидкости 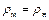 , КПД модели и натуры приблизительно одинаковы
, КПД модели и натуры приблизительно одинаковы 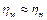 . При этих допущениях получим
. При этих допущениях получим
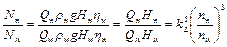
 .
.
Дата добавления: 2015-01-24; просмотров: 988;
