Определение геометрических характеристик карбюратора

Карбюратор поршневых двигателей внутреннего сгорания предназначен для создания топливно-воздушной смеси определенного состава. Поток воздуха, засасываемого в рабочие цилиндры, проходит через сужающийся воздушный канал карбюратора, в узком месте которого расположено отверстие для подачи топлива, соединенное с поплавковой камерой. Повышение скорости потока воздуха за счет уменьшения площади проходного сечения карбюратора вызывает, в соответствии с уравнением Бернулли, снижение давления. Понижение давления в месте окончания топливного канала приводит к истечению топлива в воздушный поток. Задача расчета карбюратора сводится к определению таких 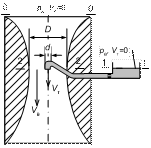его геометрических параметров, которые обеспечат необходимое соотношение топлива и воздуха в смеси.

Известны:

× соотношение между массовыми расходами топлива и воздуха 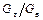, соответствующие условию полного сгорания;

× плотности топлива 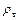и воздуха ;

× диаметр D узкого сечения воздушного канала карбюратора;

× суммарный коэффициент сопротивления воздушного канала 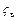и топливного 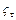с расположенным в нем жиклером.

Определить: диаметр отверстия топливного канала d, обеспечивающий заданное соотношение расходов компонентов топливно-воздушной смеси.

Запишем уравнение Бернулли для потока воздуха между сечениями 0-0 и 2-2 (параметры в сечении 2-2 обозначим индексом 2). Из-за невысокой плотности воздуха геометрическим напором, обусловленным разностью уровней рассматриваемых сечений, пренебрегаем.

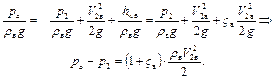
Уравнение Бернулли для потока топлива между сечениями 1-1 и 2-2 при z₁=z₂ имеет вид:

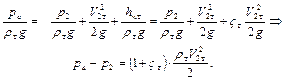
Из представленных уравнений следует, что

.

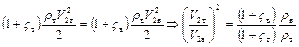Выразим скорости воздуха и топлива через их массовые расходы, плотности и площади проходных сечений каналов, по которым они движутся.

Подстановка данных выражений в предыдущую зависимость приводит к следующему итоговому уравнению

.