Теоретические основы. Контроль качества в дорожном строительстве существенно отличается, от контроля качества в других областях народного хозяйства
Контроль качества в дорожном строительстве существенно отличается, от контроля качества в других областях народного хозяйства. Это связано с линейностью объектов, разнообразием замеряемых параметров, значительной изменчивостью показателей во времени по координатам.
Наибольшее распространение на строительство получил контроль. Он в достаточной степени регламентирован нормативно - техническими документами /8/, но обладает рядом недостатков и необеспечивает необходимой надежности оценки качества.
В частности, большинством нормативных документов установлено по три измерения отдельных параметров при контроле качества. Достоверность такого метода находится в пределах 35-64 % для разных контролируемых показателей.
Таким образом, в 65-36 % случаев контроль недостоверен, что приводит к неверной оценке качества производимых работ. С другой стороны, нормативные документы по контролю качества требуют измерения большого числа параметров. Учитывая необходимость ежедневного контроля, а также неоднократность измерений всех параметров в течение смены, объем проводимых измерений оказывается громадным и практически неосуществимым.
Кроме того, существующие сейчас жесткие требования, к конкретным местам контрольных измерений приводят, с одной стороны, к недостоверности оценки и способствуют тому, что дорожники тщательно подготавливают места предстоящего контроля, не уделяя должного внимания всей дороге, а с другой - к необоснованному увеличению числа испытаний.
Практически единственное направление совершенствования контроля - это переход на статистические методы. Статистические методы позволяют сократить объем контроля и обеспечить необходимую достоверность его результатов. Сокращение достигается, за счет математического планирования.
Цель лабораторной работы - плакирование контроля качества. Основными положениями планирования контроля служат установление необходимого для обеспечения достоверности объема контроля и выбор мест проведения измерений. Существенное отличие рассматриваемого способа определения объема контроля - независимость этого объема от охваченной контролем площади при достаточно высокой достоверности результатов.
Требуемое число испытаний определяют расчётом из условия обеспечения неравенства:
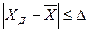 , (2.1)
, (2.1)
где 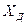 -действительное (среднее) значение генеральной совокупности;
-действительное (среднее) значение генеральной совокупности;
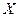 - среднее значение результатов выборки;
- среднее значение результатов выборки; 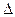 - допустимая погрешность испытаний или абсолютная ошибка.
- допустимая погрешность испытаний или абсолютная ошибка.
Совокупность всех результатов испытаний составляет вариационный ряд. Плотность нормального распределения непрерывной случайной величины 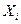 (рис. 2.1) описывается уравнением Гаусса:
(рис. 2.1) описывается уравнением Гаусса:
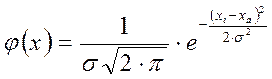 , (2.2)
, (2.2)
где 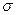 - стандартное (среднеквадратическое)отклонение; е - основание натуральных логарифмов.
- стандартное (среднеквадратическое)отклонение; е - основание натуральных логарифмов.
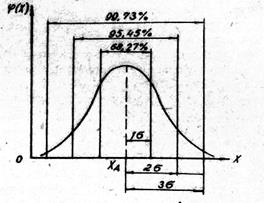
Рис. 2.1. Кривая, плотности нормального распределения
При интегрировании функции (2.2) вся площадь под кривой Гаусса при любом 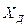 и б всегда равна I. Площадь под кривойвнутри области
и б всегда равна I. Площадь под кривойвнутри области 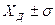 составляет 0.6827, т.е. 68,57% всей площади. Это означает, что в области
составляет 0.6827, т.е. 68,57% всей площади. Это означает, что в области 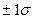 распределяются вокруг среднего значения. 68,27% результатов измерений, в области
распределяются вокруг среднего значения. 68,27% результатов измерений, в области 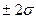 - 95,45% результатов измерений и в области
- 95,45% результатов измерений и в области 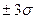 -.99,73% результатов измерений (см. рис. 2.1). Вероятность того, что значение переменной величины окажется в пределах
-.99,73% результатов измерений (см. рис. 2.1). Вероятность того, что значение переменной величины окажется в пределах 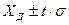 , где t - I, 2 и 3, составляет соответственно 68,27; 95,45 и 99,73. И наоборот, вероятность того, что значение переменной величины выйдет за пределы указанных интервалов, составляет 31,73; 4,55 и 0,27%.
, где t - I, 2 и 3, составляет соответственно 68,27; 95,45 и 99,73. И наоборот, вероятность того, что значение переменной величины выйдет за пределы указанных интервалов, составляет 31,73; 4,55 и 0,27%.
В дорожном строительстве приходится выполнять расчеты не только с целочисленными кратными от 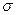 , но и проводить контроль при целочисленной статистической надежности 90, 95, 99 или 99,9%. Для этих случаев площадь под кривой определяется между границами соответственно
, но и проводить контроль при целочисленной статистической надежности 90, 95, 99 или 99,9%. Для этих случаев площадь под кривой определяется между границами соответственно 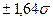 ,
, 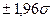 ,
, 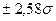 и
и 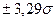 (рис. 2.2).
(рис. 2.2).
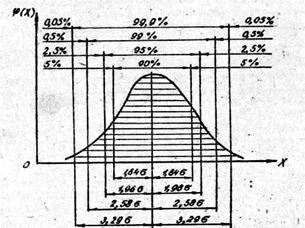
Рис. 2.2. Площади под кривой нормального распределения при целочисленных вероятностях
Для кривой распределения, по обе стороны центра группировки случайных событий можно найти предельные значения рассеяния, вероятность появления которых пренебрежимо мала. Предельные интервалы называются доверительными.
Для закона нормального распределения доверительный интервал 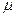 равен:
равен:
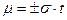 , (2.3)
, (2.3)
где t - аргумент функции Лапласа.
Из этого выражения, следует, что для повышения, надежности результатов измерений необходимо увеличить доверительный интервал. Поэтому при оценке случайной ошибки необходимо знать не только ее величину, но и значение доверительной вероятности.
Для разных категорий дорог нужна разная степень достоверности контроля, а следовательно и размер выборки, т.е., с повышением категории дороги увеличивается необходимое число испытаний. Доверительный интервал может быть двухсторонним 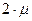 и односторонним
и односторонним 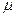 , когда по условиям эксплуатации продукции накладываются какие-либо ограничения сверху (+) или (-).
, когда по условиям эксплуатации продукции накладываются какие-либо ограничения сверху (+) или (-).
Нормируемое отклонение t определяют по табл. 2.1 в зависимости от доверительной вероятности или категории дороги, числа испытаний и вида ограничений.
Таблица 2.1. Значения нормируемого отклонения t
| Число испытаний | Значение t при одностороннем ограничении параметров для дороги категории | |||
| - | I-II | III-IV | V | |
| 4.54 | 3,18 | 2,35 | 1,64 | |
| 3.36 | 2,57 | 2,01 | 1,48 | |
| 3.00 | 2,37 | 1,90 | 1,41 | |
| 2.82 | 2,26 | 1,83 | 1,38 | |
| 2.72 | 2,20 | 1,80 | 1,36 | |
| 2.65 | 2,16 | 1,77 | 1,35 | |
| 2.60 | 2,13 | 1,75 | 1,34 | |
| 2.75 | 2,11 | 1,74 | 1,33 | |
| 2.54 | 2,09 | 1,71 | 1,33 | |
| 2.49 | 2,06 | 1,71 | 1,32 | |
| 2.46 | 2,04 | 1,70 | 1,31 | |
| 2.42 | 2,02 | 1,68 | 1,30 | |
| 2.39 | 2,00 | 1,67 | 1,30 | |
| Число испытаний | I-II | III-IV | V | - |
| Значение t при двустороннем ограничении параметров для дороги категории |
Размеры выборки (объем контроля) обосновывают с использованием методов теории вероятности, для чего применяется формула Чебышева:
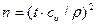
 (2.4)
(2.4)
где п - необходимое число испытаний в выборке; 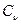 - коэффициент вариации измеряемого параметра;
- коэффициент вариации измеряемого параметра; 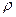 - показатель точности измерения параметра
- показатель точности измерения параметра
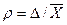 (2.5)
(2.5)
Показатель точности зависит как от метода измерения, так и от применяемых приборов. Поэтому в каждом конкретном случае его устанавливают индивидуально.
Коэффициент вариации - безразмерная, величина, характеризующая однородность измеряемого параметра и стабильность технологического процесса, которая представляет собой отношение
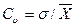 (2.6)
(2.6)
Ориентировочные значения 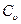 и
и 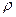 представлены в табл. 2.2
представлены в табл. 2.2
Таблица 2.2. Коэффициент вариации и показатель точности измеряемых параметров
| Наименование показателя | Коэффициент
вариации 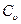
| Показатель точности 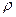
|
| Плотность грунта | 0,03 | 0,015 |
| Плотность асфальтобетона | 0,02 | 0,010 |
| Модуль упругости грунта | 0,30 | 0,100 |
| Модуль упругости слоёв дорожной одежды | 0,25 | 0,100 |
| Толщина слоёв дорожной одежды | 0,20 | 0,080 |
| Ширина слоёв, канав, половины земляного полотна | 0,10 | 0,050 |
| Просвет под трёхметровой рейкой | 0,80 | 0,200 |
| Прочность при сжатии асфальтобетонных образцов | 0,10 | 0,050 |
| Прочность при сжатии цементногрунтовых образцов | 0,15 | 0,050 |
| Влажность грунта | 0,10 | 0,050 |
| Сцепление и угол внутреннего трения в грунте | 0,10 | 0,050 |
| Температура асфальтобетона | 0,18 | 0,030 |
| Высотные отметки, глубина канав | 0,15 | 0,050 |
| Поперечные и продольные уклоны | 0,25 | 0,100 |
| Крутизна откосов | 0,38 | 0,150 |
| Уступ в швах | 0,15 | 0,050 |
| Амплитуда высотных отметок | 0,25 | 0,100 |
Второй этап подготовки контроля - планирование мест проведения измерений. Согласно положениям теории вероятностей, необходимая достоверность контроля будет достигнута лишь при случайном их выборе. Иначе говоря, при использовании статистических методов намечать точки контроля, нужно только произвольно, исключая при этом какой-либо порядок. Для соблюдения принципа случайности попользуют табличную форму случайных чисел, с помощью которой ликвидируется, всякая возможность проявления некорректности при назначении мест проведения испытаний (табл.2.3).
Таблица 2.3. Табличная форма случайных чисел
Дата добавления: 2015-01-21; просмотров: 1691;
