Методика эксперимента. При прохождении света через анизотропные среды, в частности, через кристаллы, поляризация излучения может изменяться
При прохождении света через анизотропные среды, в частности, через кристаллы, поляризация излучения может изменяться. В каждом кристалле существуют три взаимно ортогональных направления, называемые главными осями кристалла, обладающие важным свойством: если волна линейно поляризована и колебания вектора 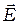 направлены вдоль одной из главных осей, то поляризация волны при прохождении через кристалл не изменяется. Для разных главных осей показатели преломления, а значит и скорости распространения волн, различны.
направлены вдоль одной из главных осей, то поляризация волны при прохождении через кристалл не изменяется. Для разных главных осей показатели преломления, а значит и скорости распространения волн, различны.
Воспользуемся этим для получения света с эллиптической поляризацией. Пусть свет проходит через кристаллическую пластинку, главные оси которой направлены по осям х и y, соответствующие показателям преломления 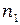 и
и 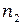 , лежат в плоскости пластинки, а третья ось z нормальна к пластинке. Направим пучок света вдоль оси z (рис.68).
, лежат в плоскости пластинки, а третья ось z нормальна к пластинке. Направим пучок света вдоль оси z (рис.68).
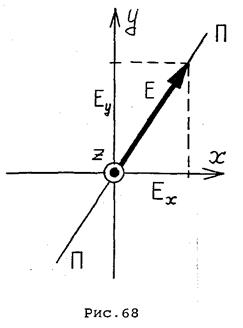
Поле 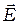 падающей волны разложим на составляющие
падающей волны разложим на составляющие
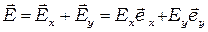
где 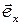 и
и 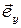 единичные векторы по осям
единичные векторы по осям 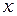 и
и 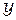 . Волна с полем
. Волна с полем 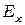 затратит на прохождение пластинки время
затратит на прохождение пластинки время 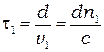 , а волна с
, а волна с  - время
- время 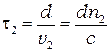 , в итоге одна волна опередит другую на время
, в итоге одна волна опередит другую на время 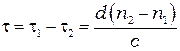 , что приведёт к дополнительному сдвигу фаз колебаний
, что приведёт к дополнительному сдвигу фаз колебаний 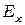 и
и 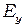 на величину
на величину
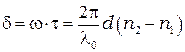
Тот же результат можно получить по-другому: для двух волн пластина создает разность хода
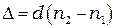
и разность фаз
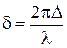 .
.
Если 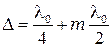 пластинку называют четвертьволновой. Если
пластинку называют четвертьволновой. Если 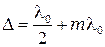 - пластинку называют полуволновой.
- пластинку называют полуволновой.
Если в линейно поляризованной падающей волне вектор 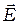 уже направлен вдоль одной из главных осей х или у, то амплитуда колебаний вдоль другой оси равна нулю, и на выходе из пластинки имеем лишь ту составляющую вектора
уже направлен вдоль одной из главных осей х или у, то амплитуда колебаний вдоль другой оси равна нулю, и на выходе из пластинки имеем лишь ту составляющую вектора 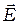 , что и на входе, т.е. поляризация волны не изменится. Если же на входе обе компоненты
, что и на входе, т.е. поляризация волны не изменится. Если же на входе обе компоненты 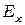 и
и 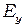 не равны нулю, то поляризация на выходе определяется соотношением их амплитуд и полученной разностью фаз
не равны нулю, то поляризация на выходе определяется соотношением их амплитуд и полученной разностью фаз 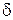 .
.
При 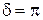 (полуволновая пластинка) синфазные колебания
(полуволновая пластинка) синфазные колебания 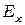 и
и 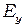 на входе в пластинку превращаются в противофазные на выходе.
на входе в пластинку превращаются в противофазные на выходе.
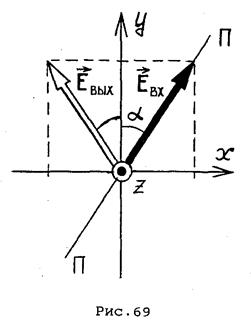
Это приводит к повороту плоскости поляризации на угол 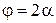 , где
, где 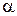 - угол между главной осью пластинки и плоскостью поляризации падающей волны (рис.69). Если повернуть пластинку вокруг оси
- угол между главной осью пластинки и плоскостью поляризации падающей волны (рис.69). Если повернуть пластинку вокруг оси 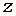 , плоскость поляризации на выходе повернется на вдвое больший угол.
, плоскость поляризации на выходе повернется на вдвое больший угол.
Если 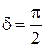 (четвертьволновая пластинка) и угол
(четвертьволновая пластинка) и угол 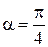 , то на выходе получим ортогональные колебания равных амплитуд (
, то на выходе получим ортогональные колебания равных амплитуд ( 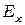 =
= 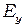 ) с фазовым сдвигом
) с фазовым сдвигом 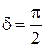 , что соответствует круговой поляризации.
, что соответствует круговой поляризации.
Если вносимая пластинкой разность хода заранее неизвестна (таков объект 39), её можно определить по анализу поляризации после пластинки следующим образом. Определим положение главных осей пластинки и установим их под углом 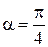 к плоскости поляризации падающего света, определяемой входным поляризатором П1 (рис. 70).
к плоскости поляризации падающего света, определяемой входным поляризатором П1 (рис. 70).
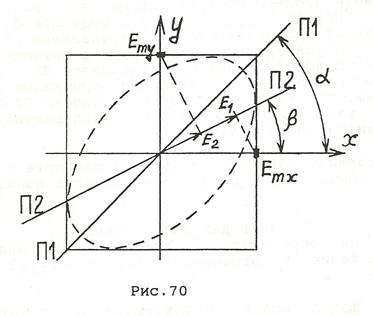
После пластинки получим колебания с одинаковыми амплитудами и со сдвигом фаз 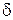 , который следует найти. Установим после пластинки поляризатор П2. Через него пройдут колебания с амплитудами
, который следует найти. Установим после пластинки поляризатор П2. Через него пройдут колебания с амплитудами
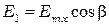 и
и 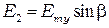 ,
,
где угол 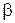 определяет ориентацию поляризатора (см. рис. 70). Интенсивность прошедшей через поляризатор волны определяется этими амплитудами, а также разностью фаз колебаний (см. методическое пособие - “Интерференция”):
определяет ориентацию поляризатора (см. рис. 70). Интенсивность прошедшей через поляризатор волны определяется этими амплитудами, а также разностью фаз колебаний (см. методическое пособие - “Интерференция”):
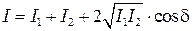
Учитывая, что 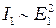 а
а 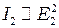 и модули амплитуды
и модули амплитуды 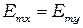 , получаем:
, получаем:
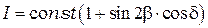 .
.
Поворачивая поляризатор П2, найдем максимальное и минимальное значение интенсивности прошедшего через него излучения. Поскольку
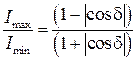
находим:
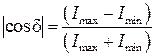 .
.
Для однозначного определения б нужно знать’ возможный диапазон значений толщины пластины. Известно, что для объекта 39 разность хода 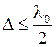 .
.
Дата добавления: 2015-01-21; просмотров: 1329;
