Oslash; Интегрирующие устройства

Могут быть электромеханическими и электронными, в них выходная величина равна интегралу от входной.

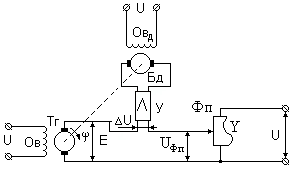
Электромеханические интеграторы могут создаваться на базе тахогенераторов (рис. 88,а). Интегрирование производится по времени. Функция интегрирования Y задана профилем функционального потенциометра Фп. У этого потенциометра сердечник выполнен с переменным сечением так, что длина витков – перемена и по длине сердечника подчиняется функции Y. Напряжение U_фп, снимаемое с потенциометра, также подчиняется закону изменения Y.

а	б
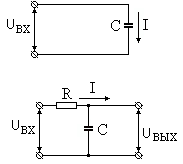
Рис. 88. Интегрирующие устройства: а – электромеханическое; б – электронные

При перемещении ламеля с постоянной скоростью v его перемещение за время t будет vt. Напряжение в этом случае

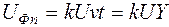, (92)

где k – коэффициент пропорциональности.

Тахогенератор механически связан с балансным серводвигателем Б_д. В статическом режиме эдс тахогенератора равна напряжению U_фп или

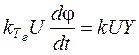, (93)

где j – угол поворота тахогенератора. Из формулы (93)

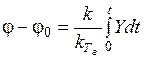, (94)

где j₀ – начальный угол поворота ротора тахогенератора.

Электронные интегрирующие устройства могут быть построены на базе емкости (рис. 88,б). Известно, что заряд на пластинах конденсатора

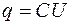, (95)

где C – емкость конденсатора, U – напряжение на его пластинах. Заряд q можно определить по выражению

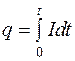. (96)

Из формул (95) и (96) получаем

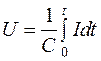, (97)

т. е. напряжение на конденсаторе пропорционально интегралу от тока. При определении выходного напряжения U_вых так же, как и в случае емкостного дифференцирующего устройства, активное сопротивление R оказывает отрицательное влияние на точность интегрирования. Окончательно

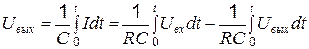. (98)

Первое слагаемое представляет собой искомый интеграл, второе – ошибку интегрирующей RC-цепи.