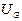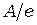МЕТОДИКА ИЗМЕРЕНИЙ

Уравнение Эйнштейна для фотоэффекта (8.3) было экспериментально подтверждено Р. А. Милликеном (1916 г.) в результате тщательно выполненных опытов.

Электроны, вылетающие из фотокатода под действием падающего света, обладают кинетической энергией и, достигая анода, создают во внешней замкнутой цепи ток.

Если в этот момент между анодом и катодом создать электрическое поле, которое тормозит фотоэлектроны, то ток будет уменьшаться. Такое тормозящее поле создается путем прикладывания к аноду отрицательного напряжения, и этот метод задерживающего потенциала обычно используется для измерения максимальной кинетической энергии фотоэлектронов.

Действительно, при увеличении абсолютного значения отрицательного потенциала на аноде U ток фотоэлектронов падает и при некотором значении 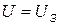(потенциал запирания) даже самые быстрые фотоэлектроны не смогут достигнуть анода, и ток в цепи прекращается. Таким образом, оказывается, что максимальная кинетическая энергия фотоэлектронов 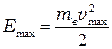связана с потенциалом запирания 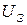таким соотношением:

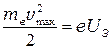(2)

Для экспериментальной проверки закона Эйнштейна в лабораторной работе измеряется зависимость электронного тока фотоэлемента от величины отрицательного задерживающего потенциала 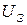на аноде. Полученная в эксперименте зависимость фототока от задерживающего потенциала, как правило, представляет собой кривую, плавно подходящую к оси абсцисс (рис. 2). Это обусловлено разбросом вылетающих из фотокатода электронов по скоростям, что в значительной степени затрудняет получение точного значения запирающего потенциала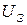

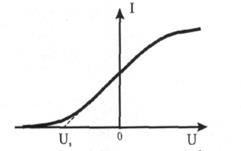
Для определения потенциала запирания 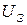предлагается подход, заключающийся в экстраполяции линейного участка вольтамперной характеристики до пересечения с осью абсцисс, как это показано штриховой линией на рис. 1.

Из выражений (1) и (2) следует, что запирающий потенциал 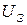находится в прямой пропорциональной зависимости от частоты света 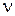, падающего на фотоэлемент:

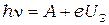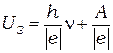или (3)

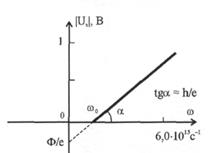
Таким образом, построив вольтамперную характеристику фотоэлемента при различных длинах волн падающего излучения и определив по ним потенциал запирания 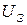, можно убедиться в линейном характер зависимости 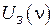. Тангенс угла наклона линейной зависимости 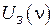к оси частот даёт оценку постоянной Планка 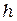. Пересечение этой прямой с осью частот даёт значение граничной частоты 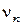, а отрезок, отсекаемый на оси 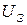, определяет работу выхода электронов 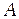из данного материала (рис. 3).