Метод частных производных

Пусть интересующая нас величина y является некоторой функцией других величин x_l, x₂, x₃ и т.д., так что

у = ƒ(x_l, x₂, x₃...) (11)

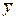
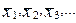причем величины x_l, x₂, x₃... мы можем измерять путем прямых измерений. В этом случае мы для определения величин и ∆ сначала измеряем все величины, от которых зависит у (x_l, x₂, x₃...) по методике, изложенной в предыдущем параграфе. В результате чего определяем , а также полные погрешности, в определении этих величин, которые обозначим как 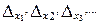Наилучшее (среднее) значение косвенно определяемой величины у находится при подстановке в (6) наилучших (средних) значений

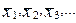
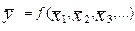
(12)

Для определения полной абсолютной погрешности величины у необходимо выяснить, как изменяется эта величина при относительно небольших изменениях всех величин, от которых зависит величина у. Это можно сделать с помощью полного дифференциала. Интересующее нас изменение величины

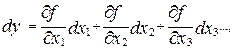(13)

где 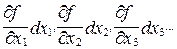- обозначают частные производные от функции f по соответствующим переменным. Эти частные производные вычисляются при наилучших (средних) значениях 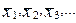и т.д.

От бесконечно малых изменений величин у, x_l, x₂, x₃... в (13) перейдем к конечным значениям их изменений

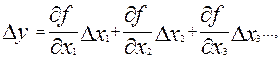(14)

где ∆y- искомая полная погрешность величины 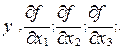- значения соответствующих частных производных, вычисленных при наилучших (средних) значениях входящих в них величин.

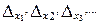- полные погрешности определения величин.

Под частной производной функции ƒ(x, y, z) по переменной X понимают величину:

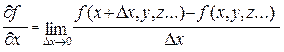(15)

т.е. это производная, которая вычисляется в предположении, что все переменные, кроме той, по которой берется производная, являются постоянными величинами. Например: пусть 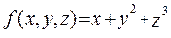. Тогда

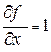
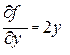
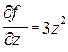
После вычисления абсолютной ошибки ∆у по формуле (14) находят относительную ошибку как

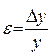(16)

Этот способ удобен в том случае, когда 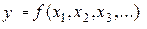представляет собой алгебраическую сумму.