Математическое описание процессов преобразования энергии в двигателе постоянного тока независимого возбуждения.
Известно, что у двигателя постоянного тока независимого возбуждения (ДНВ) обмотка возбуждения питается от независимого источника постоянного тока. Принципиальная схема этого двигателя изображена на рис.
С т.з. внутренних процессов двигатели постоянного тока независимо от способа возбуждения являются машинами переменного тока, т.к. по обмоткам их якорей течет переменный ток. Это обеспечивается работой коллектора, который коммутирует постоянных ток, идущий из сети с частотой wэл, равной электрической скорости якоря. Поэтому уравнения, описывающие процесс преобразования энергии в ДНВ, являются частным случаем обобщенного математического описания процессов электромеханического преобразования, полученного ранее.
Модели ДНВ соответствует включение обмоток двухфазной обобщенной машины по приведенной ниже схеме. Здесь обмотка статора по оси b включена на постоянное напряжение UВ, а обмотка по оси a не используется. Обмотки фаз 2d и 2q ротора питаются переменными токами i2d и i2q от преобразователя частоты ПЧ, осуществляющего коммутацию этих токов(преобразование из постоянного) в функции угла от поворота ротора jэл с частотой wэл.
 Обмотки ротора с переменными токами создают вращающееся магнитное поле, которое вращается со скоростью wэл в направлении, противоположном направлению вращения ротора. Поскольку в качестве ПЧ в машинах постоянного тока используется механический коллектор, то изображенная схема представляет модель двигателя постоянного тока. Если в качестве ПЧ используется тиристорный преобразователь частоты (ТПЧ), коммутируемый датчиком положения ротора, то это же схема является схемой модели вентильного двигателя, выполняемого на базе синхронной машины.
Обмотки ротора с переменными токами создают вращающееся магнитное поле, которое вращается со скоростью wэл в направлении, противоположном направлению вращения ротора. Поскольку в качестве ПЧ в машинах постоянного тока используется механический коллектор, то изображенная схема представляет модель двигателя постоянного тока. Если в качестве ПЧ используется тиристорный преобразователь частоты (ТПЧ), коммутируемый датчиком положения ротора, то это же схема является схемой модели вентильного двигателя, выполняемого на базе синхронной машины.
В рассматриваемой модели МДС статора создается постоянным током возбуждения iв=i1b, поэтому она ориентированна по оси b и неподвижна в пространстве. Соответственно и МДС ротора при вращении со скоростью wэл должна быть неподвижна относительно неподвижного статора. Это возможно только при условии, что МДС ротора (поле ротора) вращается относительно ротора в противоположном направлении со скоростью - wэл. Для этого нужно, чтобы обмотки фаз ротора обтекались переменными токами i2d и i2q, изменяющиеся с частотой wэл по закону: 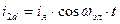
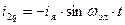 .
.
Т.к. поле ротора неподвижно относительно статора, для математического описания процессов преобразования энергии целесообразно сделать преобразование переменных машины к осям a, b для случая wк=0. С этой целью используем формулы прямого преобразования, учитывая что 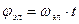 .
.
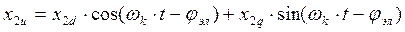
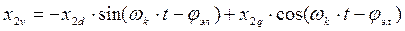 .
.
Преобразованные к осям a, b значения токов i2d и i2d получим, подставив сюда выражения i2d и i2d :

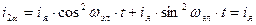
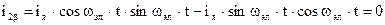
Это значит, что в осях a, b действительным переменным токам обмоток ротора эквивалентна одна якорная обмотка, расположенная по оси a, обтекаемая постоянным током iя, которая создает магнитное поле, неподвижное в пространстве и направленное по оси a, совпадающей с осью щеток двигателя. По оси b обмотки ротора нет, о чем говорит то, что ток в такой обмотке равен 0.
В реальной машине по оси щеток направлены также МДС добавочных полюсов и компенсационной обмотки (при Р>100кВт). Поэтому схема модели двигателя в осях a, b с учетом сказанного имеет вид, изображенный на рис.
Для получения уравнений динамической характеристики ДНВ воспользуемся преобразованными уравнения обобщенной машины в осях a, b.
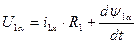
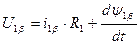
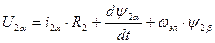
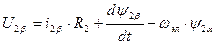
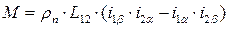
В соответствие с изображенной схемой модели ДНВ, можно принять:
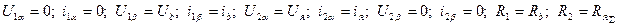
Имея это в виду и обобщенную 2-х фазную модель ДНВ, выразим потокосцепления через соответствующие токи.
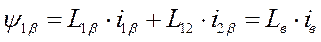
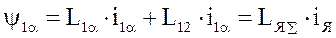
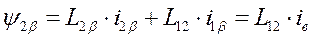
Здесь LяS - суммарная индуктивность обмотки якоря, ДП и КО.
С учетом всего этого написанные выше преобразованные уравнения будут иметь вид:
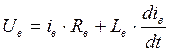
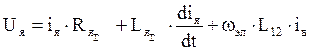
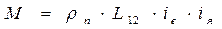
Последний член 2-го из этих уравнений – это ЭДС двигателя:
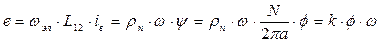
Момент двигателя:
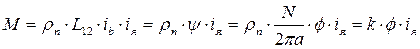
Здесь 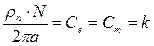 в системе СИ.
в системе СИ.
Таким образом окончательно можно записать:
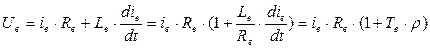
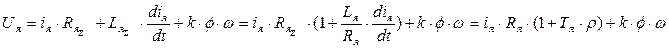
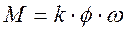
Здесь Тв, Тя – соответственно электромагнитные постоянные цепи возбуждения и цепи якоря. Обмотки ДП и КО являются вспомогательными. Поэтому в дальнейшим на схеме двигателя из изображать не будем, а их сопротивления и индуктивности учитываются в RяS и LяS.
Дата добавления: 2015-01-19; просмотров: 1036;
