Тахеометрические формулы

Тахеометрическая съемка является основным видом съемки для получения топографического плана местности в крупных масштабах (1:500 – 1:5000). Применяют ее для съемки небольших незастроенных участков местности, а также при изысканиях и проектировании дорог и искусственных сооружений.

В переводе с греческого языка тахеометрия означает „быстрое измерение“. Быстрота тахеометрической съемки достигается тем, что при одном только визировании на точку местности с исходного пункта сразу определяют расстояние до этой точки, направление на нее и превышение, что позволяет определить положение точки относительно исходного пункта в плане и по высоте.

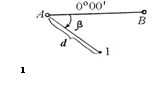Выполняют тахеометрическую съемку с помощью геодезических приборов, называемых тахеометрами. При этом расстояния до точек определяют по дальномеру тахеометра, направление линии – по горизонтальным углам, а превышения – способом тригонометрического нивелирования. Для определения планового положения точки используется полярный способ съемки, при котором положение точки 1 определятся с помощью измерения горизонтального угла (β) и полярного расстояния (d) (рисунок 1.1).

Высотное положение точки определяется путем измерения тахеометром превышения способом тригонометрического нивелирования.

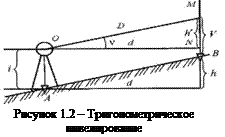Сущность тригонометрического нивелирования показана на рисунке 1.2. Для определения превышения (h) в точке А устанавливают тахеометр, а в точке 1 – рейку. Измеряют с помощью рулетки или рейки высоту прибора (i). Затем наводят зрительную трубу тахеометра на рейку и определяют по вертикальному кругу угол наклона (υ) линии визирования. С помощью дальномера тахеометра измеряют наклонное расстояние (D) или горизонтальное проложение (d).

Из рисунка 1.2 превышение (h) можно определить по формуле

h = h' + i – V , (1.1)

где h' – превышение над горизонтальным лучом визирования;

V – высота наведения на рейке (высота визирования).

Из прямоугольного треугольника OMN, видно, что

h' = d ∙ tgυ, (1.2)

или, учитывая, что

d = D ∙ cos²υ, (1.3)

получим

h' = D ∙ cos²υ ∙ sinυ / cosυ = 0,5D ∙ sin2υ. (1.4)

Окончательно с учетом формулы (1.1) превышение

h = 0,5D ∙ sin2υ + i – V.(1.5)

Если расстояние (D) измерено нитяным дальномером, то

D = kn + C, (1.6)

где k – коэффициент нитяного дальномера (k = 100);

n – число сантиметровых делений между дальномерными штрихами;

С – постоянная нитяного дальномера.

Подставив формулу (1.6) в (1.5), получим

h = 0,5(kn + C) ∙ sin2υ + i – V.(1.7)

Если при измерении углов наклона средний штрих сетки нитей тахеометра наводят на высоту прибора, то есть V = i, формулы (1.1), (1.5) и (1.7) примут более простой вид:

h = h' = d tgυ; (1.8)

h = 0,5 D sin2υ; (1.9)

h = 0,5 (kn + C) sin2υ. (1.10)

Вычисления по формулам (1.3) и (1.4) можно выполнять с помощью специальных тахеометрических таблиц, в которых по аргументам (D) и (υ) определяются горизонтальное проложение (d) и величина превышения над горизонтальным лучом (h').

При расстояниях d более 300 м в полученные формулы вводят поправку за кривизну Земли и рефракцию, которую вычисляют по формуле

f = 0,42 d² / R ,(1.11)

где d – горизонтальное проложение;

R – радиус Земли (R ≈ 6400 км).

С учетом этой поправки полная формула вычисления превышения способом тригонометрического нивелирования примет вид

h = h' + i – V + f.(1.12)

Если расстояние до определяемой точки менее 300 м, то поправка за кривизну Земли и рефракцию будет f < 0,01 м, и ее не учитывают.

Точность тригонометрического нивелирования зависит в основном от точности измерения угла наклона и величины расстояния от тахеометра до точки. В среднем при ошибке измерения угла наклона m_υ = 1' погрешность определения превышения будет составлять 4 см на каждые 100 м расстояния, то есть на 200 м m_h = 8 см.

При расстояниях свыше 1–2 км на ошибку в определении превышения начинают оказывать значительное влияние непостоянство земной рефракции и условия видимости. Поэтому тригонометрическое нивелирование следует производить в полуденное время с 9 до 16 часов, когда земная рефракция принимает более устойчивое значение.