Частотная телеграфия

Применение одноступенчатой модуляции не позволяет во многих случаях реализовать преимущества ЧТ и ФТ. Это связано с тем, что в идеальном случае полоса пропускания радиоприемника должна быть равна спектру принятого сигнала. Практически данное требование из-за нестабильности частоты несущей передатчика и частоты гетеродина приемника реализовать не удается: полосу пропускания с учетом названных нестабильностей частоты приходится расширять, что снижает помехоустойчивость. Поэтому, более продуктивным оказывается двухступенчатая модуляция, при которой логические 1 и 0 модулируют сначала поднесущую сравнительно низкой частоты, а затем этой поднесущей модулируют частоту несущей радиопередатчика. Рассмотрим более подробно такой метод двухступенчатой модуляции на примере ЧТ - ЧМ, выполняемой согласно структурной схеме, приведенной на рис. 22.3.

Рис. 22.3. Структурная схема двухступенчатой модуляции ЧТ-ЧМ

В первой ступени модуляции сигнал, поступающий от источника информации, с помощью кодирующего устройства (кодера) преобразуется в последовательность двоичных символов - в биты информации. Далее в модуляторе 1 логической 1 присваивается частота F₁, а логическому 0 - F₂ (при фазовой модуляции им присваивались бы разные значения начальных фаз). Далее синусоидальный сигнал с частотой F₁ и F₂ во второй ступени модулирует с девиацией Df_дев частоту несущей радиопередатчика. (В радиоприемнике такой сигнал дважды проходит процедуру демодуляции: сначала выделяется частота поднесущей, а затем - исходное цифровое сообщение - битовая последовательность - см. рис. 22.1, а). При такой двухступенчатой модуляции полосы пропускания фильтров, устанавливаемых в канале поднесущей частоты, удается сузить до ширины спектра передаваемого сообщения и тем самым повысить помехоустойчивость. Рассмотрим, как нужно выбирать частоты F₁ и F₂. Во-первых, следует обеспечить «плавный» переход, т.е. без скачка фазы, от сигнала с частотой F₁ к сигналу с частотой F₂ так, как показано на рис. 22.1, б. Это вызвано тем, что при скачке фазы происходит «размытие» мгновенного спектра сигнала, что снижает помехоустойчивость радиоприема и создает помехи другим системам радиосвязи. Во-вторых, значения этих частот, а точнее, соотношение между ними, должно быть таково, чтобы энергетический спектр модулированного сигнала был бы сконцентрирован в возможно узкой полосе, или не был бы «размыт». В-третьих, сигналы с частотами F_l и F₂ должны быть ортогональны. Ортогональными называют сигналы, не перекрывающиеся во времени и с несовпадающими спектральными составляющими в частотном спектре.

Введем понятие среднего значения частоты поднесущей: F₀=0,5(F₁+F₂) и разности, или дискрета частоты, DF=F₁–F₂. Тогда для частот, определяющих соответственно логические 1 и 0, запишем:

– для логической 1: F₁=F₀+0,5Df=KF_т;

– для логического 0: F₂=F₀–0,5Df=NF_т,

где F_т=1/t - частота следования элементарных посылок; К, N - числа, показывающие, сколько периодов частоты поднесущей укладывается внутри элементарной посылки, т. е. внутри одного бита, причем К>N (рис. 22.1, б).

Для дискрета частоты имеем DF=F₁–F₂=F_t(K–N).

Фазы сигналов внутри элементарных посылок на протяжении одного бита изменяются по закону:

– внутри бита логической 1: j₁(t)=2pF₁t=2pF₀t+Dj(t);

– внутри бита логического 0: j₂(t)=2pF₂t=2pF₀t+Dj(t), где дополнительное изменение фазы сигнала: Dj(t)=2p0,5DFt=pF_t(K–N)t.

К концу элементарной посылки, т.е. при t=t=1/F_t, дополнительный набег фазы на протяжении одного бита составит:

– для логической 1: Dj=+p(К–N);

– для логического 0: Dj= –p(К–N).

При К=1+N значение Dj=+p для логической 1 и Dj= –p для логического 0. Такой случай при К=4 и N=3 представлен на рис. 22.4, а, где логическая единица – F₁=4F_t; логический ноль – F₂=3F_t. Можно, например, выбрать следующие значения параметров:

t=1,28 мс или F_t=781,25 Гц; F₁=3125 Гц; F₂=2343,75 Гц.

Разложим в ряд Фурье периодическое колебание прямоугольной формы (меандр):

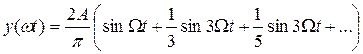. (22.1)

Рассматривая колебание (рис. 22.4,а) как сумму двух амплитудно-модулированных сигналов с частотами F₁ и F₂, с учетом последней зависимости для огибающей получим спектр, представленный при К=1+N на рис. 22.5. (Сплошные линии относятся к сигналу с частотой F₁, пунктирные - F₂.)

Рис. 22.4. Формы битовых посылок при ЧМ для 1 и 0

Из рассмотрения полученного спектра следует, что основная энергия сигнала сосредоточена в полосе DF=5F_t, а выбранные сигналы ортогональны.

Такой спектр можно еще более сузить при К=1,5 и N=1, т.е. при логической 1, представленной тремя полупериодами сигнала с частотой F₁ внутри одного бита и двумя полупериодами частоты F₂ внутри бита для логического 0 (рис. 22.4, б). При этом, согласно полученному выше выражению набег фазы на протяжении одного бита составит для логической 1: Dj = +p/2; для логического 0: Dj = –p/2. Такой случай частотной манипуляции называется манипуляцией с минимальным сдвигом (имеется в виду минимальный сдвиг фазы) - способ MSK (Minimum Shit Keying). формировать сигналы при частотной манипуляции, приведенные на рис. 22.4, можно с помощью процессора по специальной программе.

Рис. 22.5. Спектр сигнала при ЧМ битовых посылок

При этом может быть получен квазисинусоидальный сигнал, составленный из ступенек (рис. 22.6).

Рис. 22.6. Квазисинусоидальный сигнал, составленный из ступенек

При ЧМ, как и при квадратурной ФМ, можно попарно передавать биты, используя при этом четыре значения частоты, и тем самым вдвое увеличить объем информации (табл. 22.2).

Выводы по главе

1. Применение одноступенчатой модуляции не позволяет во многих случаях реализовать преимущества ЧТ и ФТ. Это связано с тем, что в идеальном случае полоса пропускания радиоприемника должна быть равна спектру принятого сигнала. Практически данное требование из-за нестабильности частоты несущей передатчика и частоты гетеродина приемника реализовать не удается: полосу пропускания с учетом названных нестабильностей частоты приходится расширять, что снижает помехоустойчивость.

Вопросы для самоконтроля:

1. В чем состоят отличия частотной и фазовой модуляции при передаче дискретных сообщений?

2. Как осуществляется двухступенчатая частотная модуляция при передаче дискретных сообщений?

3. Как выглядит сигнал с двухступенчатой частотной модуляцией при передаче дискретных сообщений?

4. Как меняется фаза сигнала при относительной фазовой модуляции?

5. Что называется квадратурной фазовой модуляцией?

Методические рекомендации.

Изучив материал главы, ответьте на вопросы. При возникновении трудностей обратитесь к материалам для закрепления знаний в конце пособия. Для углубленного изучения воспользуйтесь литературой: основной: 16 – 17; дополнительной: 4 - 6 и повторите основные определения, приведенные в конце пособия.