Спектр сигнала при частотной и фазовой модуляции

Представим выражение для ЧМ сигнала (21.6) в виде суммы двух слагаемых: u(t)=U₀ cos(m_чsinWt)cosw₀t–U₀sin(m_чsinWt)sinw₀t. (21.9)

Разложив периодические функции в (21.9) в ряд Фурье, имеем:

u(t)=U₀ J₀(m_ч)cosw₀t+U₀ J₁(m_ч)[cos(w₀+W)t–cos(w₀–W)t]+

+U₀ J₂(m_ч)[cos(w₀+2W)t–cos(w₀–2W)t]+ (21.10)

+U₀ J₃(m_ч)[cos(w₀+3W)t–cos(w₀–3W)t]+…,

где J_n(m_ч) - бесселевая функция 1-го рода n-го порядка от аргумента m_ч; n - целое число.

Пакет программ Mathcad представляет возможность путем обращения к функции J₀, J₁, J_n вычислить значения бесселевой функции 1-го рода n-го порядка при любом значении аргумента m_ч.

Согласно (21.10) при ЧМ спектр высокочастотного сигнала при тональном модулирующем сигнале частотой W имеет бесконечное число спектральных составляющих, расположенных симметрично относительно частоты w₀ через интервалы, равные W. Частоты этих спектральных составляющих равны w₀±nW, а амплитуды - U₀J_n(m_ч). Аналогичный результат получается и при фазовой модуляции с заменой параметра m_ч на Dj_дев. С помощью приведенных графиков можно построить спектр ЧМ и ФМ сигнала при заданном значении m_ч=х или Dj_дев=х. В качестве примера такие спектрограммы при m_ч=5 и m_ч=2,4 приведены на рис. 21.3.

Рис. 21.3 Спектр ЧМ и ФМ сигнала при заданном значении

m_ч=5 и m_ч=2,4

Следует заметить, что спектральная составляющая с частотой w₀, и несущая с частотой w₀ - разные понятия. Так, при m_ч=2,4 спектральная составляющая с частотой w₀ равна 0, но это не означает отсутствие несущей в сигнале. Теоретически спектр ЧМ сигнала безграничен. Однако, как показывает анализ, большая часть энергии ЧМ сигнала сосредоточена в полосе 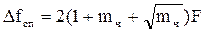, (21.11)

где F - высшая частота в спектре модулирующего сигнала.

Именно на эту величину и следует рассчитывать полосы пропускания ВЧ трактов радиопередатчиков и радиоприемников. При m_ч<<1 ширина спектра ЧМ сигнала: Df_cп=2F. ЧМ с индексом m_ч<1 является узкополосной, с индексом m_ч>2 - 3 - широкополосной. Преимущества ЧМ в полной мере реализуются при m_ч>1.