Регрессия

Регрессией называется зависимость среднего значения одной случайной величины Y от значений других исследуемых величин X_i.

Регрессионный анализ устанавливает форму зависимости между случайной величиной Y и значениями одной или нескольких переменных, причем значения эти величин считаются точно заданными. Такая зависимость определяется уравнением регрессии.

Основной этап регрессионного анализа заключается в выборе подходящей регрессионной модели, т.е. математического выражения, связывающего значения зависимой случайной величины Y и значение независимой величины X.

В простейшем случае предполагается линейная зависимость, выраженная уравнением

.

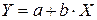b называют коэффициентом регрессии, а a – свободным членом уравнения регрессии.Параметр а является ординатой точки пересечения прямой с осью ординат, а параметр b – тангенсом угла наклона прямой относительно оси абсцисс.

Регрессия, выраженная таким уравнением, называется простой линейной регрессией. Она описывает зависимость только от одной контролируемой переменной.

Значения а и b вычисляются с помощью метода наименьших квадратов по формулам:

;

.

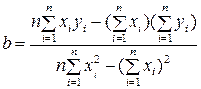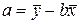Мерой точности предсказания значений случайной величины Y по заданным значениям величины X является стандартное отклонение значений y_i от регрессионной прямой, которое по-иному называется стандартной ошибкой предсказания. Стандартная ошибка предсказания вычисляется с помощью следующего соотношения:

.

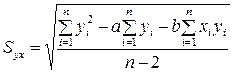Если провести две прямые, отстоящие от регрессионной прямой на расстояние ±S_yx, то они ограничат область около прямой регрессии, в которую с вероятностью 0,7 попадают экспериментальные значения y_i. Это означает, что приблизительно 70% всех значений y_i находятся в этой области.

Поскольку вычисляемый по данным исследования коэффициент регрессии является выборочным, то следует проверить его статистическую значимость. Сформулируем статистические гипотезы. Н₀ – для рассматриваемой генеральной совокупности нет статистически значимого коэффициента регрессии. Н₁ – полученный коэффициент регрессии является статистически значимым. Нулевая гипотеза Н₀ проверяется с помощью t-критерия Стьюдента, эмпирическое значение которого вычисляется с помощью соотношения

.

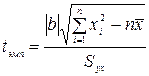Вычисленное эмпирическое значение критерия сравнивается с критическим (см. таблицу 1 Приложения) для числа степеней свободы ν=n-2 и уровне значимости α. Если t_эмп ³ t_кр, то гипотеза Н₀ отклоняется и делается вывод о значимости линейной регрессии на уровне значимости α. Если же оказывается, что t_эмп < t_кр, то принимается гипотеза Н₀.