Характеристики формы

При проведении статистических исследований встречаются распределения, имеющие самые разнообразные формы. Для характеристики отклонения формы распределения от симметричной используется коэффициент асимметрии или просто асимметрия, обозначаемая As и вычисляемая по формуле:

,

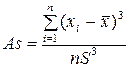где x_i - значение i-й варианты;

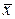- среднее арифметическое;

S - среднее квадратическое отклонение;

n - объем выборки.

Для симметричной формы распределения коэффициент асимметрии равен нулю. На рис. 8 и 9. показано два асимметричных распределения. Одно из них (рис. 8) имеет положительную асимметрию (As>0), а другое (рис. 9) – отрицательную (As<0). Иногда положительную асимметрию называют левосторонней, а отрицательную – правосторонней. Смысл этого заключается в том, что максимум распределения (и большая часть вариант) смещен влево (или соответственно вправо от значения среднего арифметического.

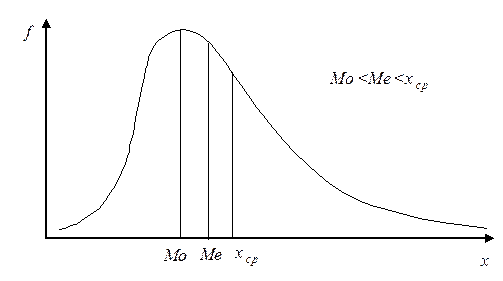
Рис. 8. Положительная (левосторонняя) асимметрия

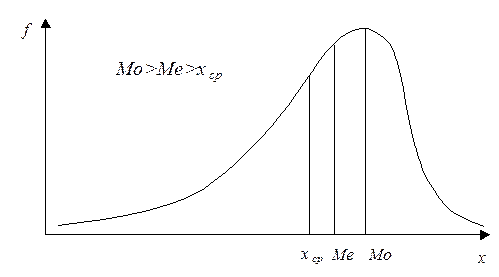
Рис. 9. Отрицательная (правосторонняя) асимметрия

Для сгруппированных данных формула для вычисления коэффициента асимметрии имеет вид:

.

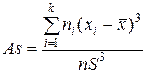Здесь n_i –частота интервала с номером i;

x_i - его срединное значение;

k - число интервалов группировки.

В рассматриваемом примере о толкании ядра:

As=[4 (13,375-14,5331)³+8 (14,045-14,5331)³+10 (14,715-14,5331)³+

5 (15,385-14,5331)5³+2 (16,055-14,5331)³]/[29* 0,7398³]= 0,260663.

Коэффициент асимметрии положителен, следовательно, можно предположить, что распределение признака в генеральной совокупности имеет левостороннюю асимметрию.

Для быстрой предварительной оценки асимметрии распределения можно воспользоваться ее простейшим показателем - мерой скошенности. Мера скошенности (Sk) определяется как отклонение среднего арифметического ( 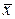) от моды (Мо):

.

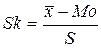Нормировка на среднее квадратическое отклонение S производится для обезразмеривания, что необходимо для сравнительного анализа степени асимметрии различных распределений. Применение этого показателя основано на том, что равенство среднего арифметического, моды и медианы имеет место только для симметричных распределений. Поэтому наиболее просто связать показатель асимметрии с соотношением характеристик положения: чем больше разница между средним арифметическим и модой, тем больше асимметрия распределения. В нашем примере:

.

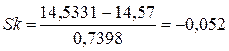Как видим, и мера скошенности имеет значение, близкое к нулю. В рассматриваемом случае As>0, а Sk<0. Никакого противоречия в этом нет, поскольку, с одной стороны, оба показателя являются выборочными, и, следовательно, вычислены с погрешностью, а, с другой стороны, оба они близки к нулю. Это соответствует случаю или симметричного распределения, или распределения, мало отличающегося от симметричного.

Следующий показатель - эксцесс - служит для характеристики так называемой крутости, т.е. островершинности или плосковершинности распределения. Эксцессом называется случайная величина, определяемая соотношением:

.

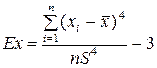Число три вычитается из частного потому, что для весьма важного и широко распространенного в природе закона нормального распределения значение этого частного равно трем. Таким образом, для нормального распределения эксцесс равен нулю. Кривые, более островершинные по сравнению с кривой нормального распределения, обладают положительным эксцессом, а кривые более плосковершинные – отрицательным эксцессом. Таким образом, нормальное распределение служит эталоном, а эксцесс показывает крутизну эмпирического распределения относительно крутизны кривой нормального распределения (см. рис. 10).

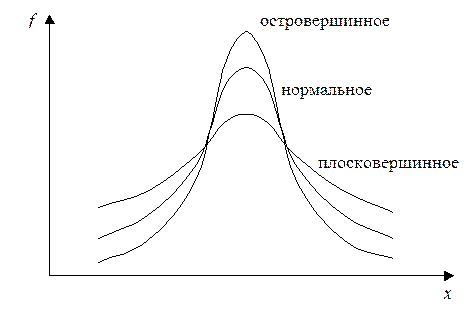
Рис. 10. Островершинное и плосковершинное распределения

Для сгруппированных данных формула для вычисления эксцесса имеет следующий вид:

.

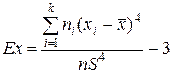В нашем примере:

Ex=[4 (13,375-14,5331)⁴+8 (14,045-14,5331)⁴+10 (14,715-14,5331)⁴+

5 (15,385-14,5331)⁴+2 (16,055-14,5331)⁴]/[29∙0,7398⁴] - 3= -0,66.

Отрицательное значение эксцесса свидетельствует о наличии тенденции к плосковершинности у рассматриваемого эмпирического распределения.