Лекция №39. Фильтри низких частот.

Цель: выдать студентам знания по теории фильтров.

Задача: научить разбираться в работе фильтров.

Рассмотрим схему простейшего низкочастотного фильтра,представленную на рис. 1,а.

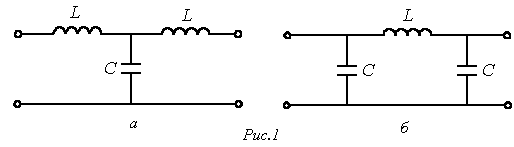
Связь коэффициентов четырехполюсника с параметрами элементов Т-образной схемы замещения определяется соотношениями (см. лекцию № 14)

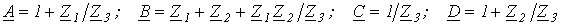
или конкретно для фильтра на рис. 1,а

;	(2)
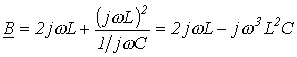;	(3)
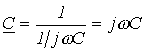.	(4)

Из уравнений четырехполюсника, записанных с использованием гиперболических функций (см. лекцию № 14), вытекает, что

.

Однако в соответствии с (2) 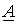- вещественная переменная, а следовательно,

.

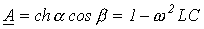(5)

Поскольку в полосе пропускания частот коэффициент затухания 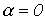, то на основании (5)

.

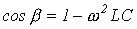Так как пределы изменения : 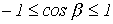, - то границы полосы пропускания определяются неравенством

,

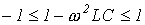которому удовлетворяют частоты, лежащие в диапазоне

.

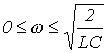(6)

Для характеристического сопротивления фильтра на основании (3) и (4) имеем

.

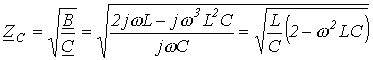(7)

Анализ соотношения (7) показывает, что с ростом частоты w в пределах, определяемых неравенством (6), характеристическое сопротивление фильтра уменьшается до нуля, оставаясь активным. Поскольку, при нагрузке фильтра сопротивлением, равным характеристическому, его входное сопротивление также будет равно 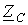, то, вследствие вещественности 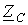, можно сделать заключение, что фильтр работает в режиме резонанса, что было отмечено ранее. При частотах, больших 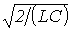, как это следует из (7), характеристическое сопротивление приобретает индуктивный характер.

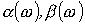На рис. 2 приведены качественные зависимости и .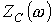

Следует отметить, что вне полосы пропускания 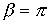. Действительно, поскольку коэффициент А – вещественный, то всегда должно удовлетворяться равенство

.

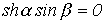(8)

Так как вне полосы прозрачности 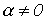, то соотношение (8) может выполняться только при .

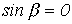В полосе задерживания коэффициент затухания 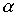определяется из уравнения (5) при 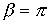. Существенным при этом является факт постепенного нарастания 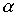, т.е. в полосе затухания фильтр не является идеальным. Аналогичный вывод о неидеальности реального фильтра можно сделать и для полосы прозрачности, поскольку обеспечить практически согласованный режим работы фильтра во всей полосе прозрачности невозможно, а следовательно, в полосе пропускания коэффициент затухания 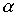будет отличен от нуля.

Другим вариантом простейшего низкочастотного фильтра может служить четырехполюсник по схеме на рис. 1,б.