Лекция №40. Полосовые фильтры. Фильтры высоких частот.
Цель: выдать студентам знания по теории фильтров.
Задача: научить разбираться в работе фильтров.
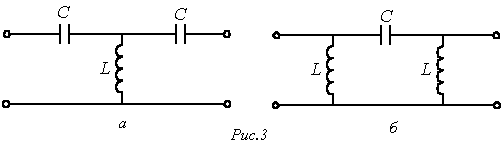
Схема простейшего высокочастотного фильтраприведена на рис. 3,а.
Для данного фильтра коэффициенты четырехполюсника определяются выражениями
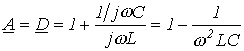 ; ;
| (9) |
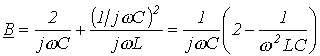 ; ;
| (10) |
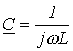 . .
| (11) |
Как и для рассмотренного выше случая, А – вещественная переменная. Поэтому на основании (9)
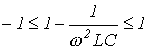 .
.
Данному неравенству удовлетворяет диапазон изменения частот
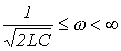 . .
| (12) |
Характеристическое сопротивление фильтра
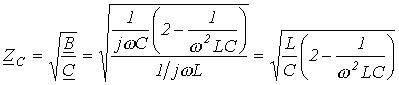 , ,
| (13) |
 изменяясь в пределах от нуля до
изменяясь в пределах от нуля до 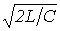 с ростом частоты, остается вещественным. Это соответствует, как уже отмечалось, работе фильтра, нагруженного характеристическим сопротивлением, в резонансном режиме. Поскольку такое согласование фильтра с нагрузкой во всей полосе пропускания практически невозможно, реально фильтр работает с
с ростом частоты, остается вещественным. Это соответствует, как уже отмечалось, работе фильтра, нагруженного характеристическим сопротивлением, в резонансном режиме. Поскольку такое согласование фильтра с нагрузкой во всей полосе пропускания практически невозможно, реально фильтр работает с 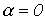 в ограниченном диапазоне частот.
в ограниченном диапазоне частот.
Вне области пропускания частот 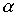 определяется из уравнения
определяется из уравнения
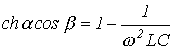
| (14) |
при 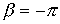 . Плавное изменение коэффициента затухания в соответствии с (14) показывает, что в полосе задерживания фильтр не является идеальным.
. Плавное изменение коэффициента затухания в соответствии с (14) показывает, что в полосе задерживания фильтр не является идеальным.
Качественный вид зависимостей 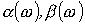 и
и 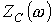 для низкочастотного фильтра представлен на рис. 4.
для низкочастотного фильтра представлен на рис. 4.
Следует отметить, что другим примером простейшего высокочастотного фильтра может служить П-образный четырехполюсник на рис. 3,б.
Полосовой фильтрформально получается путем последовательного соединения низкочастотного фильтра с полосой пропускания 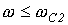 и высокочастотного с полосой пропускания
и высокочастотного с полосой пропускания 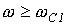 , причем
, причем 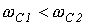 . Схема простейшего полосового фильтра
. Схема простейшего полосового фильтра
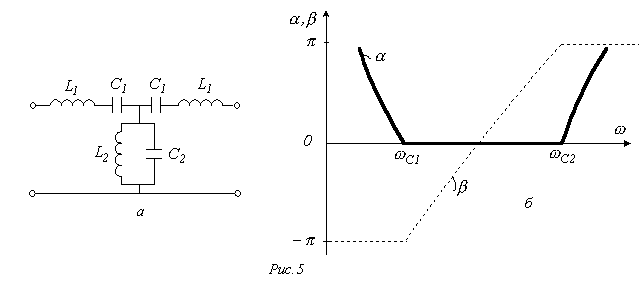
приведена на рис. 5,а, а на рис. 5,б представлены качественные зависимости 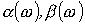 для него.
для него.
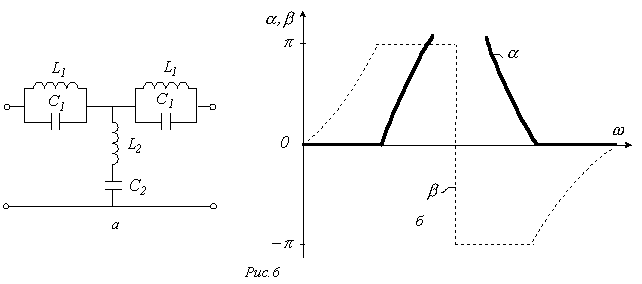
Урежекторного фильтраполоса прозрачности разделена на две части полосой затухания. Схема простейшего режекторного фильтра и качественные зависимости 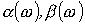 для него приведены на рис.6.
для него приведены на рис.6.
В заключение необходимо отметить, что для улучшения характеристик фильтров всех типов их целесообразно выполнять в виде цепной схемы, представляющей собой каскадно включенные четырехполюсники. При обеспечении согласованного режима работы всех n звеньев схемы коэффициент затухания 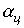 такого фильтра возрастает в соответствии с выражением
такого фильтра возрастает в соответствии с выражением 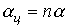 , что приближает фильтр к идеальному.
, что приближает фильтр к идеальному.
Контрольные вопросы и задачи
- Для чего служат фильтры?
- Что такое полосы прозрачности и затухания?
- Как классифицируются фильтры в зависимости от диапазона пропускаемых частот?
- В каком режиме работают фильтры в полосе пропускания частот?
- Почему рассмотренные фильтры нельзя считать идеальными?
- Как можно улучшить характеристики фильтра?
- Определить границы полосы прозрачности фильтров на рис. 1,а и 3,а, если L=10 мГн, а С=10 мкФ.
Ответ: 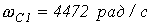 ,
, 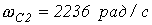 .
.
Дата добавления: 2015-03-26; просмотров: 2443;
