Математическое описание МПА
Математическое моделирование МПА следует выполнять на основе решения интегрального уравнения относительно двумерного распределения токов по плоскости антенны с ядром, зависящим от свойств материала подложки, такой подход является наиболее точным и реализован в ряде стандартных пакетов (MWOffice, Agilent и др.). Вместе с тем, существует ряд упрощенных подходов к расчету характеристик МПА, позволяющих с инженерной точностью оценить основные полевые характеристики. Одним из таких подходов является метод, разработанный Дернеридом, сводящийся к аналогии между МПА и отрезком длинной линии, нагруженным с двух сторон на резистивные и емкостные элементы. Резистивные элементы эквивалентны потерям на излучение, двух щелей с длиной равной ширине МПА W (рис. 7.1, а), расположенных на расстоянии равном длине элемента L, емкостные элементы описывают краевой эффект (емкость между концом полосковой линии передачи и проводящим основанием).
Резонансная частота 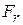 прямоугольной МПА зависит от геометрии антенны (прежде всего длины элемента L) и диэлектрической проницаемости подложки и определяется по формуле
прямоугольной МПА зависит от геометрии антенны (прежде всего длины элемента L) и диэлектрической проницаемости подложки и определяется по формуле 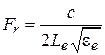 , где с – скорость света;
, где с – скорость света; 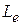 – эффективная длина излучателя;
– эффективная длина излучателя; 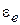 – эффективная диэлектрическая проницаемость, которая отличается от проницаемости материала подложки, поскольку поле МПА присутствует как в диэлектрике, так и в воздухе. Эти величины вычисляется по формулам:
– эффективная диэлектрическая проницаемость, которая отличается от проницаемости материала подложки, поскольку поле МПА присутствует как в диэлектрике, так и в воздухе. Эти величины вычисляется по формулам:
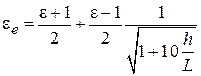 ;
;
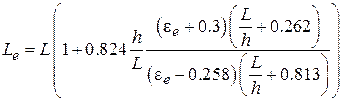 .
.
Здесь 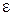 – диэлектрическая проницаемость материала подложки;
– диэлектрическая проницаемость материала подложки; 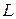 – длина элемента;
– длина элемента; 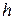 – толщина подложки.
– толщина подложки.
Увеличение диэлектрической проницаемости подложки при фиксированной геометрии элемента приводит к понижению резонансной частоты. В ряде случаев в целях уменьшения габаритов антенных систем прибегают к использованию материалов подложки с относительной диэлектрической проницаемостью от 2 до 10. Одновременно с этим уменьшение размеров МПА ведет к сужению полосы рабочих частот и уменьшению КНД.
Диаграмма направленности МПА определяется как: 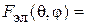
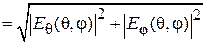 , где
, где 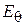 и
и 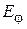 – угломестная и азимутальная компоненты поля излучения:
– угломестная и азимутальная компоненты поля излучения:
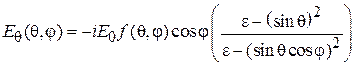 ;
;
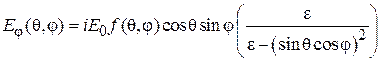 ;
;
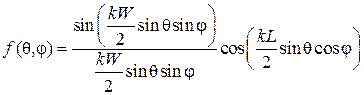 . (7.1)
. (7.1)
Здесь 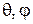 – угол места и азимутальный угол сферической системы координат;
– угол места и азимутальный угол сферической системы координат; 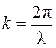 – волновое число;
– волновое число; 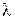 – длина волны в воздухе; W – ширина МПА;
– длина волны в воздухе; W – ширина МПА; 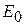 – постоянная, зависящая от амплитуды возбуждения.
– постоянная, зависящая от амплитуды возбуждения.
Диаграмма направленности антенной решетки вычисляется в соответствии с теоремой перемножения как произведение множителя системы 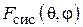 на ДН одного элемента
на ДН одного элемента 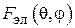 :
:
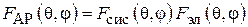 (7.2)
(7.2)
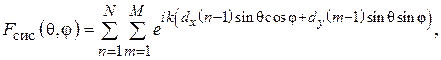 (7.3)
(7.3)
где 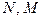 – число элементов в решетке по одной и другой координатам (в данном случае
– число элементов в решетке по одной и другой координатам (в данном случае 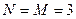 , общее число элементов в решетке равно произведению
, общее число элементов в решетке равно произведению 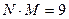 );
); 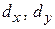 – периоды антенной решетки (т. е. расстояние между центрами элементов) по координатам х и у соответственно, для исследуемой в работе АР
– периоды антенной решетки (т. е. расстояние между центрами элементов) по координатам х и у соответственно, для исследуемой в работе АР 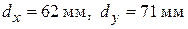 .
.
Дата добавления: 2015-03-26; просмотров: 1142;
