Решение. Число появлений события A: m = 70.

Число испытаний: n = 200.

Число появлений события A: m = 70.

Вероятность появления события A: p = 0,3, значит q = 1 – p = 0,7.

Величина npq = 200∙0,3∙0,7 = 42.

Так как npq > 20, то можно воспользоваться приближенным равенством из локальной теоремы Муавра-Лапласа:

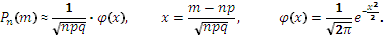
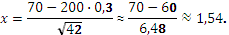
По таблице значений функций Гаусса (приложение 1) находим:

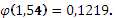
Тогда: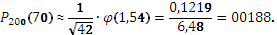

Ответ: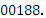

11) Вероятность появления события A в каждом из 200 независимых испытаниях постоянна и равна 0,3. Найти вероятность того, что событие A появится не более 70 раз.