Концентрация растворов
Важнейшей характеристикой количественного содержания компонентов в системе является концентрация растворов.
Концентрацией растворовназывают определенное массовое (или объемное) содержание растворенного вещества в определенном массовом (или объемном) количестве растворителя или раствора.
Существуют несколько методов выражения концентрации растворов. Рассмотрим самые распространенные из них (табл.3.1).
Таблица 3.1
| Методы выражения концентрации растворов | Обозначение и размерность применяемых величин |
Массовая доля растворенного вещества – это отношение массы растворенного вещества к общей массе раствора:
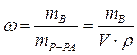
| 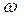 - массовая доля растворенного вещества, безразмерная величина - массовая доля растворенного вещества, безразмерная величина
|
| mВ - масса растворенного вещества, г | |
| mР-РА - масса раствора, г | |
| V - объем раствора, мл | |
| ρ -плотность раствора, г/мл | |
Процентная концентрация:
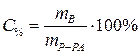
| С% - процентная концентрация, % |
| m В - масса растворенного вещества, г | |
| mР-РА - масса раствора, г | |
Молярная концентрация, или молярность,– число молей растворенного вещества в 1 дм3
(1 литр) раствора:
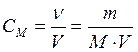
| СМ - молярная концентрация , или молярность; иногда обозначают М |
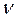 - количество (число моль) растворенного вещества, моль - количество (число моль) растворенного вещества, моль
| |
| V - объем раствора, дм3 (л) | |
| mВ - масса растворенного вещества, г | |
| МВ - молярная масса растворенного вещества, г/моль |
Для более рационального решения предложенных задач можно применять вспомогательные формулы (табл.3.2).
Таблица 3.2
| Формула | Применение |
| mР-РА = V·ρ | Для вычисления массы раствора |
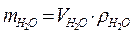
| Для воды 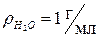 при 4 оС (1мл = 1 см3) при 4 оС (1мл = 1 см3)
|
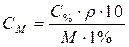
| Для перехода от процентной к молярной концентрации |
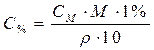
| Для перехода от молярной к процентной концентрации |
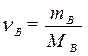
| Для нахождения количества вещества |
| m1Р-РА+ m2Р-РА= mР-РА | При сливании двух растворов различных концентраций массы первого и второго растворов складываются |
| m1В+ m2В= mВ | При сливании двух растворов различных концентраций массы растворенных веществ, содержащихся в растворах, складываются |
| m1В= m2В | При разбавлении растворов водой масса вещества, содержащегося в растворе, остается неизменной |
При решении задач необходимо обращать особое внимание на размерность применяемых величин и обязательно приводить их в соответствие друг другу. Поэтому при подстановке численных значений в формулы надо указывать размерность величин. Решение задач оформлять обязательнов соответствии с приведенными ниже примерами.
Дата добавления: 2015-01-15; просмотров: 1246;
