Пример. 2. Обработка КВД с учетом притока жидкости к забою после ее остановки по интегральному методу Э.Б.Чекалюка.
После установившейся работы скважины с дебитом нефти Q0 = 200 т/сут на забое скважины дифференциальным глубинным манометром снята кривая восстановления давления, а также кривые восстановления давления на буфере ( 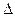 рбуф) и в затрубном пространстве скважины (
рбуф) и в затрубном пространстве скважины ( 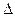 рзат), см. табл. 8.2. Эффективная толщина пласта равна 10 м и коэффициент пористости — 0,2. Свойства нефти:
рзат), см. табл. 8.2. Эффективная толщина пласта равна 10 м и коэффициент пористости — 0,2. Свойства нефти: 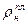 = 810 кг/м3;
= 810 кг/м3; 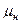 = 2,2 мПа·с;
= 2,2 мПа·с; 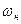 = 1,38;
= 1,38; 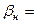 10,5·10-5 см3/кгс;
10,5·10-5 см3/кгс; 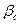 = 1·10-5 см2/кгс. Площадь сечения столба жидкости в подъемных трубах Fтp = 30 см2, а в затрубном пространстве Fзат = 135 см2.
= 1·10-5 см2/кгс. Площадь сечения столба жидкости в подъемных трубах Fтp = 30 см2, а в затрубном пространстве Fзат = 135 см2.
Таблица 8.2
Результаты исследования скважины
| t, с | 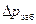 , кгс/см2 , кгс/см2
| 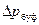 , кгс/см2 , кгс/см2
| 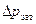 , кгс/см2 , кгс/см2
| V (t), м3 |
| 9,32 12,08 13,35 14,10 14,70 15,10 15,49 15,70 15,90 16,09 16,40 16,75 16,97 17,20 17,50 17,65 | 6,6 7,7 8,8 9,5 10,1 10,7 11,1 11.5 12,2 12,7 13,6 14,7 15,4 16,0 16,9 17,5 | 2,6 3,6 4,1 4,4 4,5 4,5 4,5 4,5 4,5 4,5 4,5 4,5 4.5 4,5 4,5 4,5 | 1,215 1,585 1,710 1,79 1,87 1,93 2,00 2,02 2,04 2,06 2,08 2,12 2,15 2,17 2,19 2,20 | |
Примечание.1 кгс/см2 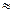 0,1 МПа 0,1 МПа
|
В последней графе табл. 8.2 приведены результаты подсчета по формуле (7.22) притока в ствол скважины нефти V(t)после ее остановки. Например,
для t = 600 с
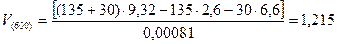 м3;
м3;
для t = 1200 с
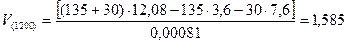 м3
м3
Для построения кривой восстановления давления в координатах y, x определим координаты четырех точек при четырех значениях времени 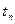 , например при
, например при 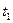 =1800с,
=1800с, 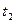 =3600,
=3600, 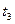 =6000 и
=6000 и 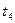 =10800 с. Примем масштаб времени п =
=10800 с. Примем масштаб времени п = 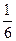 . Тогда безразмерное время
. Тогда безразмерное время  будет равным
будет равным
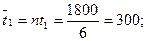
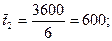
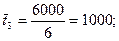
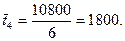
По данным табл. 8.2 составляем вспомогательную табл. 8.3 для четырех принятых значений времени.
Значения величин G( 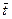 ) находятся по величинам
) находятся по величинам 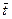 с помощью палеток (см. рис. 7.3).
с помощью палеток (см. рис. 7.3).
Для каждого из безразмерных 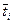 строятся кривые зависимости
строятся кривые зависимости 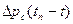 от G(t) (рис. 8.2).
от G(t) (рис. 8.2).
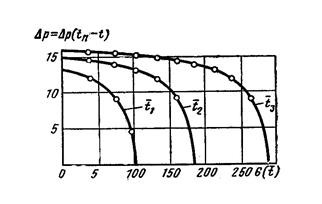
Рис. 8.2. Кривые зависимости  от G(
от G( 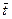 ) для
) для  = 300;
= 300;  = 600;
= 600;  = 1000.
= 1000.
По этим кривым находятся значения интегралов Дюамеля в соответствии с формулой (7.23). Площадь заключенную между каждой из кривых и координатными осями, делят на вертикальные полосы принятой постоянной ширины, а интеграл определяют как произведение сумм средних ординат для каждой из полос на ширину полосы, например:
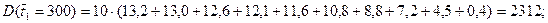
Таким же образом получают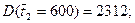
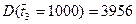 и
и 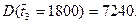
Величины 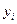 (левая часть уравнения (7.18) рассчитываются следующим образом:
(левая часть уравнения (7.18) рассчитываются следующим образом:
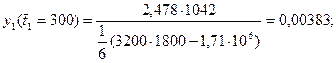
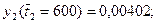
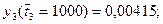
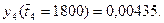
Величины 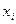 определяются логарифмированием ti:
определяются логарифмированием ti:
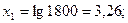
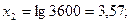
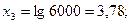
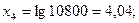
По точкам в координатах yi, хi, проводим прямую (рис. 8.3), отсекающую на оси ординат отрезок у0 == 0,00158 и расположенную к оси абсцисс с уклоном
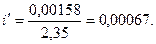
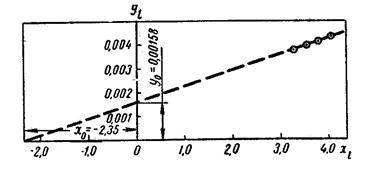
Рис. 8.3. Зависимость yi от хi, построенная с учетом притока жидкости в скважину после остановки.
Дата добавления: 2015-01-15; просмотров: 1379;
