ЛЕКЦИИ 5,6
При расчете зубьев на прочность по напряжениям изгиба вводят следующие допущения:
• Нагрузка передаётся одной парой зубьев и приложена к вершине зуба.
• Зуб рассматриваем как консольную балку, для которой справедлива
гипотеза плоских сечений.
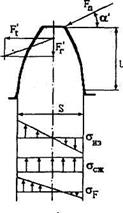
Рис.3.5
Действующие силы:
· сила нормального давления в точке контакта зубьев 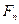 (3.5);
(3.5);
· окружная сила 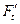
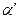 - угол направления нормальной силы. Угол
- угол направления нормальной силы. Угол 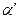 несколько больше угла
несколько больше угла 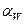 :
: 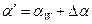
Перенесём силу 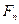 на ось симметрии зуба и разложим её на составляющие:
на ось симметрии зуба и разложим её на составляющие:
| I |
 ;
;
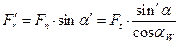
Напряжение изгиба в опасном сечении, расположенном вблизи хорды основной окружности:
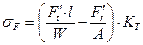 (3.19)
(3.19)
где 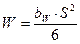 - момент сопротивления;
- момент сопротивления;
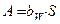 - площадь;
- площадь;
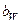 - ширина зубчатого венца;
- ширина зубчатого венца;
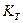 - теоретический коэффициент концентрации напряжений.
- теоретический коэффициент концентрации напряжений.
За расчётные напряжения принимают растягивающие напряжения, так как в большинстве случаев усталостные трещины возникают здесь. Размерные величины 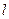 и
и 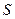 неудобные для расчета. Так как зубья различного модуля геометрически подобны, то величины
неудобные для расчета. Так как зубья различного модуля геометрически подобны, то величины 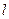 и
и 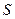 выражают через безразмерные величины:
выражают через безразмерные величины:
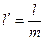 и
и 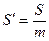 .
.
где 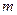 - модуль зубьев.
- модуль зубьев.
Подставим ввыражение (3.19) для расчёта напряжений изгиба в опасном сечении значения всех составляющих. Получим:
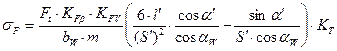 , (3.20)
, (3.20)
где 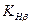 - коэффициент неравномерности нагрузки;
- коэффициент неравномерности нагрузки;
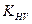 - коэффициент динамической нагрузки при расчёте зубьев на изгиб.
- коэффициент динамической нагрузки при расчёте зубьев на изгиб.
Введём обозначение:
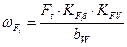 - удельная расчетная окружная сила;
- удельная расчетная окружная сила;
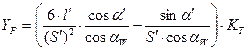 - коэффициент формы зуба.
- коэффициент формы зуба.
Величина 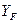 зависит от числа зубьев и коэффициента смещения исходного контура и определяется по специальным графикам. С учётом этих обозначений условие прочности на изгиб запишется:
зависит от числа зубьев и коэффициента смещения исходного контура и определяется по специальным графикам. С учётом этих обозначений условие прочности на изгиб запишется:
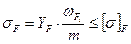 (3.21)
(3.21)

Полученная формула (3.21) является основной для проверочного расчёта прямозубой передачи. Для проектных расчётов эту формулу разрешают относительно модуля. Выражая окружную силу 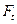 через вращающий момент на шестерне
через вращающий момент на шестерне 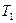 и принимая
и принимая 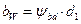 из условия (3.21), найдем
из условия (3.21), найдем
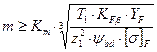 (3.22)
(3.22)
где 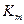 - коэффициент. Можно принять для прямозубой передачи
- коэффициент. Можно принять для прямозубой передачи 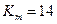 .
.
Значения модуля округляют до ближайшего значения из ряда модулей по ГОСТ 9563-60 и по принятому значению модуля находят размеры колес. Ширина шестерни в прямозубой передаче выполняется несколько больше номинальной ширины для компенсации неточностей установки в осевом направлении.
Из формулы (3.22) видно, что модуль и, как следствие, габариты передачи могут быть уменьшены за счет повышения прочности материала колес, а также путем уменьшения концентрации нагрузки вдоль зуба (уменьшения 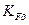 и увеличения
и увеличения  ).
).
Колеса с малым модулем зацепления предпочтительны по условиям плавности и экономичности, однако крупномодульные колеса менее чувствительны к перегрузкам, неоднородности материала и погрешности изготовления в меньшей степени влияют на прочность зубьев. Поэтому для силовых передач значения 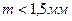 принимать не следует.
принимать не следует.
ЛЕКЦИИ 5,6
Краткое содержание
Фрикционные передачи. Достоинства фрикционных передач. Недостатки фрикционных передач. Основные требования к материалам фрикционных катков. Расчет фрикционных передач. Ременные передачи. Достоинства ременных передач. Недостатки ременных передач. Типы ремней. Усилия в передаче. Порядок проектного расчёта плоскоременной и клиноременной передач. Конструкции шкивов.
Дата добавления: 2015-03-23; просмотров: 965;
