Понятие о статической и динамической устойчивости

 Прямой критерий статической устойчивости простейшей электрической системы
Прямой критерий статической устойчивости простейшей электрической системы
Выделим из электрической системы одну генераторную ветвь и предположим, что в системе постоянны частота ( 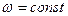 ) и напряжение в узловой точке
) и напряжение в узловой точке 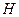 (
( 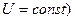 .
.
Тогда схема замещения рассматриваемой генераторной ветви будет иметь вид, показанный на рис. 4.1.
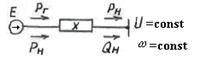 Рис.4.1. Схема исследуемой системы
Рис.4.1. Схема исследуемой системы
Выражения для активной и реактивной мощностей в начале и конце передачи с учетом (2.10) имеют вид:
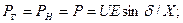 (4.1)
(4.1)
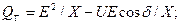 (4.2)
(4.2)
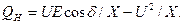 (4.3)
(4.3)
Предполагая, что меняется только угол 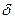 (
( 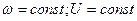 ) построим серии характеристик
) построим серии характеристик 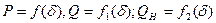 при изменении
при изменении  (рис.4.2) согласно выражениям (4.1)
(рис.4.2) согласно выражениям (4.1) 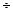 (4.3).
(4.3).
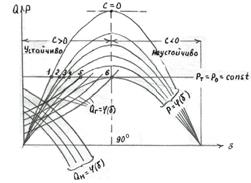 Рис.4.2. Характеристики мощности
Рис.4.2. Характеристики мощности
Сделанное предположение, что величины 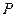 и
и 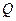 зависят только от значения угла
зависят только от значения угла 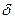 в данный момент и не зависят от того, каким образом было достигнуто это значение, озачает, что рассматриваемая система является позиционной.
в данный момент и не зависят от того, каким образом было достигнуто это значение, озачает, что рассматриваемая система является позиционной.
Далее предположим, что мощность турбины генератора не зависит от изменений угла 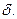 Тогда можно записать, что отклонение (небаланс) мощности генератора при каких-либо случайных малых изменений в системе (например, изменение угла
Тогда можно записать, что отклонение (небаланс) мощности генератора при каких-либо случайных малых изменений в системе (например, изменение угла 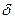 , частоты
, частоты 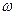 и напряжения
и напряжения 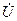 ) будет
) будет
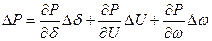 ,
,
которое с учетом принятых выше условий ( 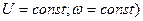 перепишется как
перепишется как
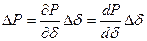 . (4.4)
. (4.4)
Обозначая 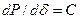 , определим отклонение угла
, определим отклонение угла 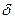 при появлении небаланса мощности
при появлении небаланса мощности 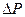 :
:
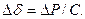 (4.5)
(4.5)
Согласно выражению (4.5) можно утверждать, что при 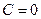 будет наступать критический режим, так как при ничтожно малом изменении
будет наступать критический режим, так как при ничтожно малом изменении 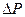 изменение угла
изменение угла 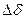 будет получать очень большие значения (
будет получать очень большие значения ( 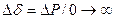 ).
).
Легко установить (из раннее приведенных рассуждений), что при положительных значениях 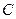 система устойчива, а при отрицательных – неустойчива.
система устойчива, а при отрицательных – неустойчива.
Таким образом, прямой критерий критического (по текучести или сползанию) режима простейшей системы имеет вид
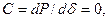 (4.6)
(4.6)
а условие устойчивости имеет вид
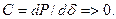 (4.7)
(4.7)
Заметим, что в технической литературе соотношение 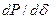 часто называют синхронизирующей мощностью.
часто называют синхронизирующей мощностью.
Дата добавления: 2015-03-23; просмотров: 1479;
