Метод симметричных составляющих. В соответствии с этим методом любую систему трех несимметричных векторов можно разложить на три системы векторов:
В соответствии с этим методом любую систему трех несимметричных векторов можно разложить на три системы векторов:
- симметричную систему трех векторов прямой последовательности,
- симметричную систему трех векторов обратной последовательности,
- симметричную систему векторов нулевой последовательности.
Графически это можно представить так, как показано на 4.1.
Аналитически это можно записать в следующем виде:
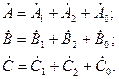 (4.1)
(4.1)
Из приведенной системы (4.1) видно, что она содержит 9 неизвестных векторов (составляющих исходной трехфазной несимметричной системы векторов), которые связаны между собой тремя уравнениями. Решение системы уравнений (4.1) в представленном виде невозможно.
Для ее решения следует воспользоваться свойствами систем симметричных составляющих: в каждой трехфазной системе симметричных составляющих векторы фаз А, В, и С одинаковы по модулю; векторы фаз систем симметричных составляющих прямой и обратной последовательностей сдвинуты относительно друг друга на 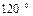 , а векторы фаз нулевых составляющих одинаково направлены.
, а векторы фаз нулевых составляющих одинаково направлены.
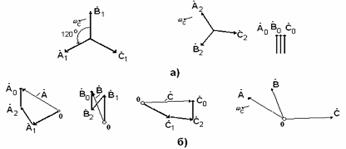 Рис.4.1.
Рис.4.1.
а- трехфазные системы векторов прямой, обратной и нулевой последовательностей;
б – порядок получения исходных фазных векторов и исходной несимметричной трехфазной системы векторов.
Для решения системы (4.1.) нужно ввести единичный вектор 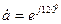 , позволяющий свести систему (4.1) к системе трех уравнений с тремя неизвестными
, позволяющий свести систему (4.1) к системе трех уравнений с тремя неизвестными 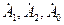 .
.
Дело в том, что если любой вектор умножить на 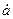 , то модуль вектора не изменится, а лишь произойдет его поворот на угол
, то модуль вектора не изменится, а лишь произойдет его поворот на угол 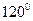 против направления движения стрелки часов.
против направления движения стрелки часов.
Таким образом систему (4.1) можно переписать в следующем виде:
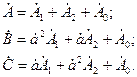 (4.2)
(4.2)
Учитывая что 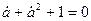 , получим при решении (4.2) следующие соотношения:
, получим при решении (4.2) следующие соотношения:
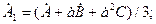 (4.3)
(4.3)
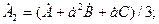 (4.4)
(4.4)
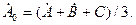 (4.5)
(4.5)
Таким образом, было показано, что, если система (4.1) позволяет по известным симметричным составляющим фазных величин определить несимметричные векторы исходной трехфазной системы, то соотношения (4.3)-(4.5) позволяют решить обратную задачу – определить по известным несимметричным векторам трехфазной системы их симметричные составляющие.
Согласно ГОСТ абсолютную величину отношения составляющей обратной последовательности к составляющей прямой последовательности называют коэффициентом несимметрии исходной системы, то есть

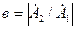 , (4.6)
, (4.6)
а абсолютную величину отношения составляющей нулевой последовательности к составляющей прямой последовательности называют коэффициентом неуравновешенности системы
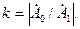 . (4.7)
. (4.7)
Как следует из рис.4.1, системы векторов прямой и обратной последовательностей являются симметричными и уравновешенными. Система векторов нулевой последовательности является симметричной, но неуравновешенной.
Понятию систем векторов – токов прямой, обратной и нулевой последовательностей соответствует понятие сопротивлений прямой последовательности 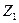 , обратной последовательности
, обратной последовательности 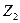 и нулевой последовательности
и нулевой последовательности 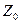 .
.
Условились считать, что генератор создает только э.д.с. прямой последовательности, а э.д.с. обратной и нулевой последовательностей следует учитывать в виде падений напряжения с обратным знаком, которые приложены к точке к.з.
Поэтому для точки к.з. связь между симметричными составляющими напряжения и падениями напряжений для различных последовательностей будет (например, для фазы 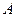 , принимая, что
, принимая, что 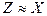 ):
):
 ; (4.8)
; (4.8)
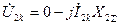 ; (4.9)
; (4.9)
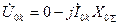 . (4.10)
. (4.10)
Как следует из (4.8)-(4.10) каждое соотношение связывает два неизвестных:  и
и 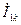 ,
, 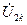 и
и 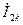 ,
, 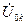 и
и 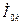 и в таком виде эти соотношения не могут быть решены.
и в таком виде эти соотношения не могут быть решены.
Для решения соотношений (4.8)-(4.10) необходимы еще три уравнения, некоторые определяют из начальных условий для конкретных случаев несимметрии.
Заметим, что понятия напряжения, токи и сопротивления различных последовательностей условны. Эти понятия возникают из сущности метода расчета – метода симметричных составляющих.
Дата добавления: 2015-03-23; просмотров: 1153;
