Прийняття господарських рішень у конфліктних ситуаціях

Ситуація конфлікту є невід’ємною складовою ринкового середовища, під час якої кожен із суб’єктів (конкурентів) намагається завдати збиток іншому та мінімізувати власні витрати. Конфлікт­ною називається ситуація, коли стикаються інтереси двох чи більше сторін, які мають суперечливі цілі, причому виграш кожної зі сторін залежить від того, як поводитимуться інші [31; 58]. Приклади конфліктних ситуацій: «бойові» дії, біржові угоди, різні види виробництва в умовах конкуренції, угоди на фондовому ринку, спортивні змагання, змагання, ігри. У житті конфлікт завжди супроводжується ризиком.

Рішення в умовах конфлікту завжди пов’язані з ризиком, тому необхідним є обґрунтований підхід у виборі напряму подальших дій. Підприємець у процесі своїх дій повинен вибрати таку стратегію, що дасть змогу йому зменшити ступінь протидії, що, у свою чергу, знизить ступінь ризику.

Математичний апарат для вибору відповідного господарського рішення в конфліктній ситуації сформований у теорії ігор. Завдяки їй:

ü підприємець або менеджер краще розуміють конкретну обстановку, проблему в цілому та зводять до мінімуму ступінь ризику;

ü можна вирішувати багато економічних проблем, пов’я­заних з вибором, визначенням найкращого стану, підпорядкованого тільки деяким обмеженням, що випливають з умов самої проблеми;

ü підприємець (менеджер) спонукується розглядати всі можливі альтернативи як своїх дій, так і стратегії партнерів, конкурентів.

Мета теорії ігор — формування рекомендацій щодо оптималь­ної поведінки учасників конфлікту, тобто визначення оптимальної стратегії кожному з них. У теорії ігор розроблено систему власних понять [31]. Математична модель конфлікту називається грою, сторони у конфлікті — гравцями. Результат гри називаєтьсявиграшем, програшем абонічиєю, правила гри — перелік прав і обов’язків гравців. Ходом називається вибір гравцем однієї з перед­бачених правилами гри дій. Ходи бувають особисті та випадкові. Особистий хід — це свідомий вибір гравця, випадковий хід — вибір дії, що не залежить від його волі. Залежно від кількості мож­ливих ходів у грі ігри поділяються на скінченні та нескінченні.Скінченні — ті, котрі передбачають нескінченну кількість ходів, нескінченні — навпаки. Деякі ігри в принципі мають вважатися скінченними, але мають так багато ходів, що належать до нескінченних (шахи).

Стратегією гравця називається сукупність правил, що визначають вибір варіанту дій у кожному особистому ході. Оптимальною стратегією гравця називається така, що забезпечує йому макси­мальний виграш. Ігри, що складаються тільки з випадкових ходів, називаються азартними. Ними теорія ігор не займається. Її мета — оптимізація поведінки гравця у грі, де поряд з випадковими є особисті ходи (стратегічні ігри). Гра називається грою з нульовою сумою, якщо сума виграшів усіх гравців дорівнює нулю, тобто кожен виграє за рахунок інших. Гра називається парною, якщо в неї грають два гравці. Парна гра з нульовою сумою називається антагоністичною.

Основне припущення, на підставі якого знаходять оптимальне рішення в теорії ігор, полягає в тому, що супротивник такий же розумний, як і сам гравець. У грі грають два гравці, назвемо їх А і B. Себе прийнято ототожнювати з гравцем А. Нехай в А є m можливих стратегій: 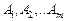, а в супротивника B — n можливих стратегій: 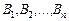. Така гра називається грою 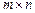. Позначимо через 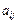виграш гравця A за власної стратегії 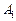і стратегії супротивника 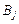. Зрозуміло, що можлива кількість таких ситуацій — .

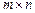Гра може мати нормальну (матричну) форму або розгорнуту (у вигляді дерева). Гру зручно відображати таблицею, що називається платіжною матрицею, або матрицею виграшів (табл. 5.2). Платіжна матриця має стільки стовпців, скільки стратегій у гравця B, і стільки рядків, скільки стратегій у гравця A. На перетині рядків і стовпців, що відповідають різним стратегіям, стоять виграші гравця A і, відповідно, програші гравця B.

Зведення гри до матричної форми саме по собі може бути важ­ким і навіть нездійсненним завданням унаслідок незнання стратегій, величезної їх кількість, а також через складність оцінювання виграшу. Ці приклади і мають на меті показати обмеженість даної теорії, тому що в усіх подібних випадках задача не може бути розв’язана методами теорії ігор.

Таблиця 5.2