Теорія корисності в системі процесів прийняття рішень

Проблема раціонального вибору є однією з головних економіч­них задач. Її постійно розв’язують основні суб’єкти економіки — виробники та споживачі. Виробники намагаються найвигідніше вкласти капітал у виробництво товарів, які приносять дохід. Споживачі бажають придбати продукцію з високою споживчою цінністю та за прийнятною ціною. Кожна з цих задач розв’я­зується в умовах ризику. Результати рішень залежать від випадкових величин, які характеризуються ймовірнісними функціями розподілу. Для того, щоб порівнювати їх ефективність, необхідно вміти порівнювати функції розподілу ефективності. Для задач прийняття рішень в умовах ризику та невизначеності принцип оптимального вибору часто описується за допомогою функції корисності.

Корисністьвиражає ступінь задоволення особи від споживання товару чи виконання будь-якої дії. В економічному аналізі корисність часто застосовується для того, щоб описати пріоритет у ранжуванні наборів споживчих товарів і послуг. Основним припущенням економічної теорії є припущення про те, що людина завжди робить раціональний вибір. Поняття функції корисності дає можливість зіставити споживчий ефект від купівлі (продажу) різних, навіть фізично несумісних, товарів (ефект від купівлі однієї сорочки й однієї книги). Корисність розглядається як певним чином узагальнені втрати чи виграші, коли всі цінності зведено до однієї шкали. Корисність вимірюють у довільних одиницях, що називаються одиницями корисності, які можна пов’язати з іншими одиницями, наприклад, грошовими. Цей зв’язок і визначає величину корисності для особи, що приймає рішення. Людина завжди обирає той варіант, корисність якого, на її думку, максимальна. Функцією корисності

називається деяка функція 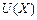, визначена на множині переваг, якщо вона монотонна, тобто з того, що 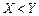, випливає 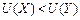. Цінні папери та майбутні інвестиції також є товаром, тому, з одного боку, їх ефектив­ності можна розрахувати, бо вони мають грошову оцінку. Але ризикові цінні папери або інвестиції гарантують отримання грошей у майбутньому, і тут зіставити їх ефективність неможливо. Встановлення будь-якого ступеня ризику, характеризуючи випадкову величину одним числом, є спробою подолати цю суперечність.

Аксіоми раціональної поведінки наведено у праці Дж. Фон Ней­мана та О. Моргенштерна. За умови виконання цих аксіом автори довели теорему про існування деякої функції, що регулює раціональний вибір, — функції корисності [31].

Аксіома 1 (повноти). Коли підприємець стикається з двома будь-якими рядами подій, він завжди може сказати, який йому більше до вподоби або йому байдуже, який із рядів подій вибрати. Ця аксіома записується у вигляді:

— X ≥ Y (X більше до вподоби, ніж Y, або байдуже);

— X ≈ Y (X і Y рівноцінні);

— X > Y (X більше до вподоби, ніж Y).

Завдяки аксіомі повноти споживач наділяється здатністю класифікувати (розрізняти) ряди подій, тобто вмінням порівнювати всі альтернативи.

Аксіома 2 (транзитивності). Перевага серед різних рядів подій послідовна, тобто, якщо ряд X > Y, Y > Z, то X > Z. Завдяки аксіомі транзитивності виключається мінливість смаків споживача.

Припустимо, що споживач віддає перевагу ряду подій f над рядом d, а ряду d над рядом b, ряду b над рядом подій f.

Отже, щоб господарювання було раціональне, підприємець повинен мати усталений смак, інакше він ніколи не зможе зробити правильний вибір.

Аксіома 3 (неперервності). В умовах аксіоми транзитивності відносно альтернатив X, Y, Z припустимо, що з імовірністю 1 індивід може отримати Y, з імовірністю p — X, а з ймовірністю (1 – p) — Z. Тоді існує таке p, за якого ці дві лотереї для індивіда рівноцінні.

Аксіома 4 (незалежності). Нехай існують блага або товари X і Y, які, на думку індивіда, однакові, та дві лотереї, які відрізняються лише тим, що одна містить X, а друга — Y, тоді ці дві лотереї для індивіда однакові.

Аксіома 5 (нерівних імовірностей). Якщо індивіду запропонувати дві лотереї, які дають однаковий виграш із різною ймовірніс­тю, то він обирає ту, ймовірність виграшу якої більша.

Аксіома 6 (складеної лотереї). Коли призом однієї лотереї є білет іншої лотереї, то індивід приймає рішення лише з міркувань імовірностей виграшу кінцевого призу.

Для визначення корисності використовують поняття лотереї [8]. Для цього експерту пропонують порівняти дві альтернативи:

1) значення показника X;

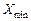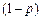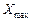2) лотерею: отримати з імовірністю або з ймовірністю — .

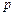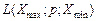Величину ймовірності 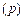змінюють поступово до такої величини від 0 до 1, доки, на думку експерта, значення показника 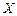і лотерея 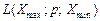стануть еквівалентними. Тобто всі можливі результати розміщують за зростанням. Корисність найгіршого результату оцінюється як 0, а найкращого — 1 (або як 100): .

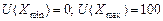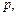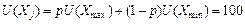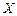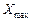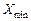Для того щоб оцінити проміжний результат, особі пропонують взяти участь у лотереї. Значення за якого особа відмовиться від гарантованого результату на користь участі у лотереї, беруть для розрахунку корисності: . Тобто із множини значень відомого показника експерт повинен розрахувати два: і — найбільш пріоритетне і найменш пріоритетне, для яких 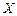не гірше з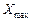а , а 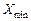не гірше за .

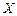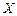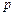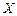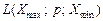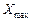Корисність варіанту визначається ймовірністю — за якої експерту байдуже, що обирати: гарантовано або лотерею , де і 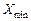— вектори, найбільш і найменш приоритетні порівняно з 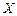. Наприклад, маємо два варіанти:

1) отримати гарантовано 100 грн;

2) узяти участь у лотереї: або одержати 50 грн з імовірністю 0,4, або отримати 150 грн із відповідною ймовірністю 0,6.

Для кожної людини буде своє значення ймовірності, за якої їй байдуже, що обирати: гроші гарантовано або участь у лотереї. Імовірність перетворюють на корисність, помножуючи на 100, якщо корисність визначається за 100-бальною шкалою, або помножуючи на 10, коли за 10-бальною.

Нехай лотерея 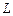приводить до виграшів (подій) 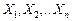із відповідними ймовірностями 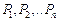і відповідними корисностями .

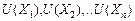Математичне сподівання виграшу, тобто очікуваний виграш, обчислюють за формулою:

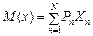. (4.1)

Математичне сподівання корисності, тобто очікувану корисність, визначають за формулою:

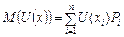. (4.2)

Корисність результатів збігається з математичним сподіванням корисності результатів.

Взаємозв’язок ризику з функціями корисності визначається поняттям детермінованого еквіваленту. Детермінований еквівалент лотереї — це гарантована сума 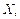отримання якої еквівалентно участі в лотереї і гарантує особі таку саму корисність, як і участь у ризикованій справі, тобто

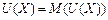.(4.3)

Особу, що приймає рішення, називають несхильною до ризику, коли для неї найбільш пріоритетною є можливість одержати гарантовано очікуваний виграш у лотереї, ніж узяти в ній участь.

Із теорії корисності можна зробити висновок, що корисність лотереї збігається з математичним сподіванням корисності її випадкових результатів. Відповідно до цього умова несхильності до ризику набуває такого вигляду:

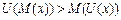, (4.4)

тобто корисність сподіваного доходу більше сподіваної кориснос­ті. ОПР не схильна до ризику тоді й тільки тоді, коли її функція корисності увігнута.

Для функції корисності можна розрахувати премію за ризик у лотереї(p(х)) як різницю між очікуваним виграшем і детермінованим еквівалентом:

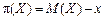.(4.5)

За своїм фізичним змістом премія за ризик (надбавка за ризик) — це сума в одиницях виміру показника X, якою суб’єкт управління згоден поступитися із середнього виграшу, щоб уник­нути ризику, пов’язаного з лотереєю, і отримати гарантований дохід без ризику.

Коли особа, що приймає рішення, натрапляє на лотерею, менш пріоритетну, ніж стан, у якому вона в даний момент перебуває, то постає питання, скільки б вона заплатила (в одиницях вимірювання критерію X) за свою неучасть у цій лотереї (уникнення її).

Страхова сума (CC) — це величина детермінованого еквівалента з протилежним знаком:

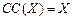. (4.6)

Умова схильності до ризикунабуває такого вигляду:

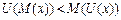, (4.7)

тобто корисність сподіваного доходу менше сподіваної кориснос­ті. ОПР схильна до ризику тоді й тільки тоді, коли її функція корисності опукла, а графік розгорнутий дзвоном униз. Премія за ризик у випадку схильності до ризику показує, скільки коштів інвестор може додатково отримати або втратити, ризикуючи.

Умова байдужості до ризику набуває такого вигляду:

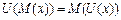. (4.8)

ОПР байдужа до ризику тоді й тільки тоді, коли її функція корисності лінійна, а графік — пряма.Премія за ризик у випадку байдужості до ризику завжди дорівнює нулю.

У теорії ринку цінних паперів широко використовується квадратична функція корисності вигляду:

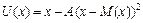, (4.9)

де А — задане число.

Зміст цієї функції такий: інвестор вважає корисним для себе збільшити значення ефективності, але бажає уникнути відхилення цієї ефективності від сподіваного значення. Чим більше А, тим більше тенденція запобігання ризику, тобто А — міра несхильнос­ті до ризику, а 1/А — міра схильності до ризику.

За допомогою функції корисності можна розраховувати ймовірність банкрутства:

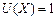, якщо ,

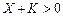або 0, якщо ,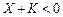

де K — початковий капітал.

Методика побудови функції корисності для будь-якого економічного показника складається з таких кроків:

Крок 1. Виявити найкращі та найгірші з можливих допустимих показників і присвоїти їм значення корисності відповідно 100 і 0 (якщо корисність оцінюється за 100-бальною шкалою).

Крок 2. Розглянути кілька проміжних показників і вказати їхнє значення корисності (кожним експертом окремо).

Крок 3. Розрахувати середні оцінки корисності проміжних значень, вказаних експертами.

Крок 4. Якщо спостерігається розсіювання значень якогось із показників, то потрібно повернутися до кроку 2, аби узгодити думки експертів для досягнення прийнятного діапазону розсіювання оцінок (кроки 2—4 можуть повторюватися кілька разів).

Крок 5. Визначення функції корисності через побудову функції регресії методом найменших квадратів (простіша функція корисності — рівняння прямої). Вид і аналітична форма функції корисності свідчить про відношення суб’єкта, що приймає рішення, до ризику.