ВВЕДЕНИЕ В СТРАТЕГИЧЕСКИЙ МЕНЕДЖМЕНТ

Частота (довжина хвилі у вакуумі) лазерного випромінювання визначається властивостями активного середовища й параметрами оптичного резонатора. Математичній вираз електричного поля лазерного випромінювання має вид

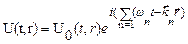
Спектр випромінювання (кількість мод у випромінюванні ) залежіть від геометричних властивостей резонатора й активного середовища може бути:

- багаточастотним (n>1) або одночастотним (n=1) у залежності від значення міжмодового інтервалу – 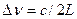, та шириною полоси посилення активного середовища.

- багатомодовим або одномодовим (висші моді ТЕМ_nm) у залежності від діафрагми в резонаторі.

У тому випадку, коли реалізується одночастотний та одномодовий режим можна ввести такий параметр як ширина лінії випромінювання 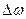. Ця величина залежить від природної ширині 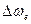та технічної ширині 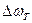лінії випромінювання

Природна ширина спектральної лінії 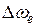набагато менше технічної, 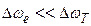. Тому у лазерів поведінка частоти випромінювання залежить від технічної ширини. Величина 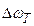різна для різних типів лазерів. Перехід до високостабільних систем, наприклад таким, як лазери, стабілізовані за надвузкими оптичними резонансами в атомах і молекулах, дозволяє одержати ширину спектральної лінії ~0,5 Гц. У випадку високостабільних лазерів, технічні флуктуації зменшуються и таким чином природні флуктуації, стають істотними. Форма природної спектральної лінії є лоренцівська з шириною, яка описується виразом [111]

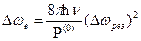
(1.1)

Технічна ширина 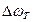формується за рахунок природних флуктуацій для опису яких використовується модель гаусових флуктуації:

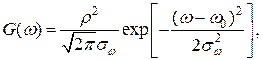
(1.2)

де 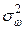- дисперсія частоти,

.

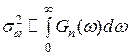Тому вираз для технічної ширини має вигляд 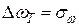, підкреслюючи цим, що причиною розширення лінії в розглянутому випадку виявляються фактори технічного порядку, внесок яких залежить від конструкції лазера, стабілізації параметрів тощо.

Потрібно враховувати, що характеристикою «часова когерентність» визначають довжину часового цугу 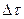, протягом якого джерело є монохроматичним. Довжина когерентності - відстань 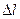відповідному поширенню хвилі протягом часу когерентності .

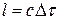Час когерентності й довжина когерентності вводяться також і для багаточастотного випромінювання. (Голографія). Але тоді, ширина частотного спектра визначається кількістю мод у випромінюванні.

Для одержання необхідних частотних характеристик у першу чергу необхідно домагатися звуження технічної ширини лінії випромінювання. На наступному етапі шляхом використання природних ліній поглинання охолоджених атомів і іонів домагаються звуження природної ширини лінії випромінювання.

Лазери можуть бути зі стабілізацією частоти випромінювання по природних оптичних частотних реперах.

У таких лазерах к основним частотним характеристикам відносяться:

- номінальне значення частоти поглинання, обумовлене квантовими переходами, що беруть участь як оптичні репери;

- відтворюваність частоти випромінювання;

- нестабільність частоти випромінювання.

Загальне, широко використовуване, рівняння осцилятора, у якого існують малі статистичні модуляції амплітуди й фази

.

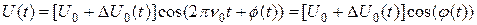(1.3)

Миттєва частота являє собою похідну від фази коливань:

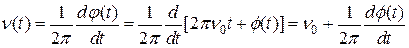
(1.4)

Динамічна складова миттєвої частоти визначається через залежну від часу фазу .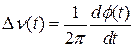

Для зручності опису стандартів частоти, що працюють на різних оптичних частотах 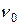, зазвичай використовується нормована фаза:

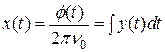
(1.5)

Часова похідна фази 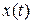являє собою нормований частотний зсув

.

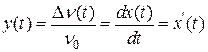(1.6)

Безперервна нормована функція 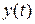описує часову залежність флуктуацій частоти 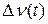. У процесі послідовного виконання 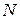вимірів величини 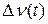, які здійснюються звичайно за допомогою частотомірів, що працюють в радіодіапазоні, установлюється ряд дискретних значень 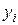. ( 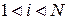). Оскільки кожний вимір частоти за допомогою частотомірів здійснюється протягом часу усереднення 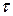, що є встановлюваним параметром частотоміра, то величина 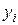являє собою .

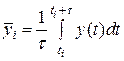У практиці частотних вимірів звичайно послідовність 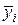представляє ряд випадкових значень.

Тому для них можна ввести середнє значення:

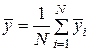
(1.7)

стандартне відхилення:

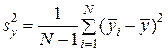
(1.8)

і стандартне відхилення середнього:

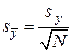
(1.9)

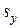- величина, що представляє собою ширину гістограми 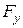, побудованої по величинах 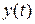або , які згруповані в межах смуг із шириною .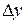

Часто флуктуації 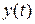представляють результат впливу статистичних процесів. Якщо ці процеси стаціонарні, то відповідно до центральної граничної (предельной) теореми теорії ймовірностей 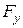трансформується в гаусову функцію щільності ймовірності 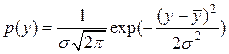с варіацією 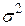. Тому властивості статистичних процесів забезпечують оцінку очікуваного значення 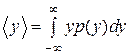і варіації .

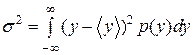Використовуючи вираз для очікуваного значення, вираз для 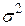можна записати в такий спосіб:

(1.10)

Очікуване значення 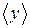й варіація 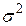статистичного процесу може бути тільки оцінене за допомогою кінцевої послідовності флуктуючої величини, для якої 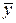оцінює очікуване значення 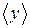гаусового процесу, а стандартне відхилення 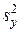оцінює варіацію .

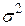Крім того, визначення величини середнього й стандартного відхилення за результатами вимірів частоти одиночного осцилятора аналогічно середньої величини й стандартному відхиленню, що може бути визначене по статистичному усередненню ідентичних осциляторів. Фактично можливість використання такої умови випливає з ергодичності випадкових процесів, що впливають на поводження частоти осциляторів.

Використання статистичних методів для визначення середнього значення й стандартної девіації зустрічається із труднощами, якщо застосовуються до флуктуючих величин з кореляцією.

Для того щоб зробити оцінку середнього статистичного процесу при наявності кореляції необхідно встановити характеристики процесу вимірів. Так якщо кількість виконаних вимірів - 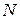, час вимірів - 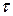, час між початковими моментами окремих вимірів - (варто врахувати, що звичайно мертвий час 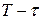між вимірами величина позитивний), то можна ввести варіацію в наступному виді:

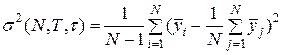
(1.11)

Дисперсія Алана 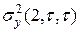являє собою двоточковудисперсію й за умови 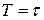й описується таким виразом:

.

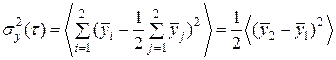(1.12)

Дисперсія Алана та її квадратний корінь, яку іноді називають стандартне відхилення Алана, ґрунтується на відмінності суміжних частотних значень вірніше, ніж частотні відмінності від середнього значення.

Альтернативою дисперсії Алана може бути визначення через девіацію фази або девіацію нормалізованої фази 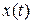. Для заданого інтервалу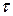

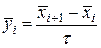
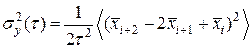
(1.13)

1.2 Особливість виміру абсолютних частот лазерного випромінювання за допомогою спектра випромінювання фемтосекундного лазера

Звичайно, відтворюваність частоти (довжини хвилі) важлива характеристика, але для лінійних вимірів необхідно знати абсолютне значення довжини хвилі випромінювання (абсолютну частоту оптичного випромінювання). Для виміру абсолютних оптичних частот створювалися радіочастотні мости й з їхньою допомогою дотепер вимірювали частоту лазерів в оптичному діапазоні. Сучасна техніка для виміру оптичних частот заснована на технології з використанням фемтосекундних лазерів. Слід зазначити, що розвиток цей технології (комбтехнології) тільки почався, тому вартість експериментального обладнання дуже висока. Із-за цього роботи з фемтосекундними лазерами не стали ще широкомасштабними. Щоб виміри з використанням цієї техніки абсолютне значення оптичної частоти необхідно знати параметри оптичного дискретного спектру випромінювання імпульсного лазера.

Імпульсне лазерне випромінювання фемтосекундної тривалості і його спектральні характеристики мають ряд специфічних властивостей.

У часовій області:

1. Імпульс являє собою коливання несучої оптичної частоти протягом інтервалу часу порядку с.

2. Обвідна імпульсу, тобто обвідна коливань несучої частоти, має максимум, що у часі не збігається з максимумом коливань несучої частоти.

3. Часове зрушення 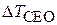між зазначеними максимумами знаходиться через різницю фази несучої частоти щодо обвідної імпульсу (рис. 1).

Подібні зрушення фази неминуче виникають у реальному лазері через різницю між фазовою і груповою швидкостями випромінювання в резонаторі лазера.

У частотній області:

1. Послідовність оптичних імпульсів описується дискретним частотним спектром, ширина 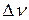якого визначається через тривалість одиночного імпульсу – 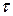, тобто 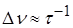. Центральна частота спектра збігається із частотою випромінювання, що відповідає максимуму смуги посилення активного середовища. Таким чином, спектр являє собою набір дискретних оптичних частот. Наприклад, довжина хвилі випромінювання імпульсного лазера на основі Ti:сапфіра, перебуває в діапазоні від 700 до 800 нм (частота ~ 400 ТГц), щодо якої розташовується дискретний набір оптичних частот. Ширина оптичного спектра досягає 20 – 30 ТГц, залежно від конструктивних особливостей лазера.

2. Дискретний спектр випромінювання імпульсного лазера фемтосекундного діапазону інакше називають частотною гребінкою (рис. 2) оптичних еквідистантно розташованих частот, тим самим підкреслюється, що Фур’є–перетворення послідовності імпульсів являє собою не суцільний, а дискретний спектр. Частота кожного окремого піка такої гребінки (або кожної спектральної складової) визначається:

– її номером 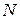, що відлічується від першої гармоніки, розташованої поблизу нуля на частотній осі;

– частотним інтервалом між піками – ;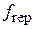

– величиною 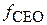–зрушенням піка з 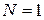«ідеальної» частотної сітки, що перекриває весь частотний діапазон, відносно 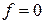. Внаслідок цього вся гребінка зрушується щодо спектра цілих гармонік частоти повторення на частоту розстроювання між несучою й що обгинає.

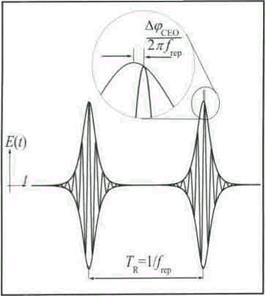
Рисунок 1. Часове подання фемтосекундних імпульсів

Частота окремого піка гребінки оптичних частот визначається виразом:

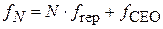. (1.14)

Абсолютне значення оптичної частоти кожного піка визначається вимірюванням значень радіочастот 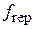і 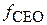, що принципово спрощує завдання вимірювання оптичних частот з максимальною точністю. Оскільки вимірювання цих частот можуть бути проведені за допомогою високоточних частотомірів, каліброваних за водневими або рубідієвими стандартами частоти, то обумовлене значення оптичної частоти буде пов’язане із частотою первинного стандарту частоти – цезієвим стандартом частоти 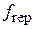, дорівнює частоті міжмодового інтервалу і звичайно лежить у діапазоні 100 – 1000 МГц. 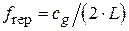, де 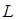– довжина резонатора, а 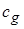– групова швидкість випромінювання усередині резонатора.

Випромінювання фемтосекундного лазера може бути представлено як сума усіх частотних компонентів:

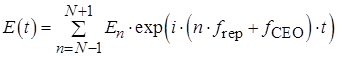. (1.15)

Звідси 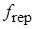може бути визначений як різниця частот сусідніх спектральних компонент:

. (1.16)

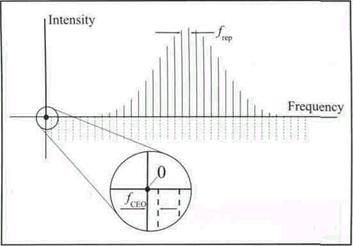
Рисунок 2. Частотна гребінка випромінювання фемтосекундного лазера

Контрольні питання за темою лекції

1. Як організувати частотні вимірювання

2. Які методи обробки результатів вимірювань використовуються при частотних вимірюваннях

3. Назвіть особливості стаціонарніх та нестаціонарніх процесів, методу стаціонарних приращень , параметра Алана.

4. Які відомі особливості характеристики спектру випромінювання фемтосекундного лазеру.

5. Як проводяться вимірювання абсолютних значень частоти лазерного випромінювання за допомогою спектру випромінювання фемтосекундного лазеру.

ВВЕДЕНИЕ В СТРАТЕГИЧЕСКИЙ МЕНЕДЖМЕНТ