Поле дислокации.
Дислокация рассматривается, как бесконечный прямолинейный объект в неограниченной однородной изотропной линейно упругой среде.
Дислокация создает такое поле смещений 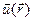 , что для контура Бюргерса любого радиуса (рис.11):
, что для контура Бюргерса любого радиуса (рис.11):
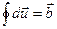
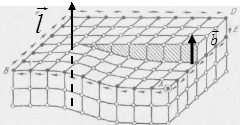
Рисунок 11. Контур и вектор Бюргерса для винтовой дислокации
Полное описание поля дает тензор деформаций
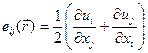 .
.
Из обобщенного закона Гука следует связь касательных σij и нормальных σii напряжений с деформацией:
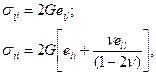
где 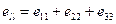 – дилатация (относительное изменение объема).
– дилатация (относительное изменение объема).
В любой точке 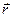 тензор деформации поля винтовой дислокации имеет вид
тензор деформации поля винтовой дислокации имеет вид
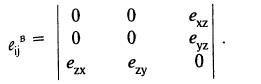
Поле краевой дислокации отличается от поля винтовой дислокацией структурой тензора:
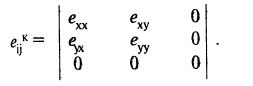
Поле винтовой дислокации находят в цилиндрических координатах r, θ, z (рис. 12) непосредственно из определения: накопление смещений uz при обходе дислокации по контуру Бюргерса составляет 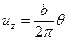 (рис. 11).
(рис. 11).
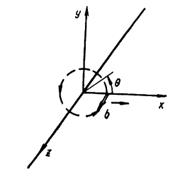
Рисунок 12. Контур Бюргерса для винтовой дислокации.
Поскольку 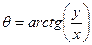 в прямоугольных координатах, дифференцируя uz, получим:
в прямоугольных координатах, дифференцируя uz, получим:
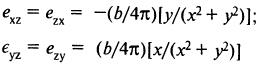
Тензор напряжений σij получается из тензора деформаций с помощью закона Гука.
Его отличие от тензора деформаций в том, что для краевой дислокации компонента 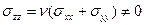 . Вместе с тем в поле винтовой дислокации нигде нет дилатации (
. Вместе с тем в поле винтовой дислокации нигде нет дилатации ( 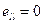 ) и гидростатического давления:
) и гидростатического давления: 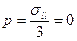 . У краевой дислокации есть и дилатация, и гидростатическое давление.
. У краевой дислокации есть и дилатация, и гидростатическое давление.
Компоненты тензора напряжений винтовой дислокации в декартовых координатах:
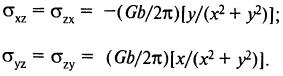
В цилиндрических координатах(r, θ), поскольку выбор направления r безразличен, положим r=x и y=0. Тогда 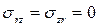 и
и 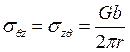 .
.
Существует всего одна пара ненулевых компонент напряжения: касательное 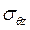 вдоль оси дислокации в плоскости, проходящей через эту ось, и парное к нему
вдоль оси дислокации в плоскости, проходящей через эту ось, и парное к нему 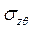 , действующее по окружности в плоскости, перпендикулярной оси. В любой системе координат с удалением от оси дислокации все напряжения монотонно убывают как
, действующее по окружности в плоскости, перпендикулярной оси. В любой системе координат с удалением от оси дислокации все напряжения монотонно убывают как 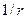 .
.
Симметрия поля краевой дислокации ниже. Если ось z направлена вдоль оси дислокации, а ось x вдоль вектора Бюргерса 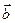 , то кроме z = const у поля смещений нет плоскостей симметрии.
, то кроме z = const у поля смещений нет плоскостей симметрии.
Компоненты поля напряжений краевой дислокации в декартовых координатах:
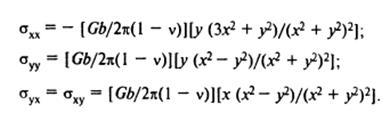
Наиболее простой вид имеет гидростатическое напряжение
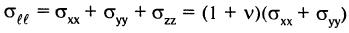
и гидростатическое давление в цилиндрических координатах
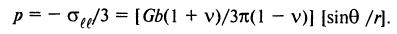
Поле смешанной дислокации с углом φ между вектором Бюргерса 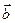 и осью z результат наложения краевой дислокации с вектором Бюргерса
и осью z результат наложения краевой дислокации с вектором Бюргерса 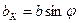 и винтовой – с той же осью
и винтовой – с той же осью 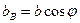 .
.
Дата добавления: 2015-03-20; просмотров: 969;
