Контур и вектор Бюргерса. Геометрические свойства.
Для количественного анализа возмущений от дислокации вокруг ее оси проводят произвольный замкнутый ориентированный контур - «контур Бюргерса».
Контур Бюргерса – это цепочка векторов, соединяющая смежные атомы.
Начало и конец контура в разрыве соединяет вектор Бюргерса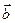 
, равный смещению, произведенному дислокацией (рис.5).
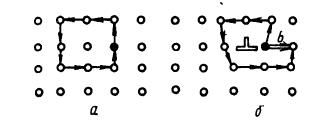
Рисунок 5. Контур Бюргерса: а- в идеальной решетке, б- в решетке с одной дислокацией.
Величина и направление 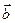не зависят от размера контура Бюргерса, его конфигурации и выбора точки начала контура.
Следствие:
1.Вектор Бюргерса 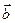- есть вектор трансляции решетки, т.к. после скольжения решетка сохраняется, т.е. собственно пластический сдвиг не сопровождается разрушением
2.Вектор Бюргерса 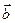может менять свою величину только скачком.
Такой скачок в некоторой точке означает, что дислокация ветвится, т.е. в этой точке встретились три дислокации (рис.6).
Рисунок 6. Ветвление дислокаций
Если ветвления нет, то 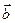остается неизменным вдоль всей длины дислокации. Следствие:
Дислокация не может обрываться внутри кристалла.
Определение дислокации №2 «Дислокацияесть линейный дефект, который разрывает любой контур Бюргерса, охватывающий его ось»
Оба определения эквивалентны. Преимущество определения №2 в удобстве описания смещений атомов из узлов в дислокации.
Знак вектора Бюргерса определяется направлением обхода по контуру Бюргерса.
Будем считать, что положительное направление оси дислокации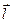 
от нас.
Обход контура будем осуществлять против часовой стрелки, тогда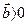 
, если его проекция на ось 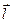положительная, т.е. 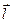∙ 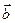=0 (рис.7).
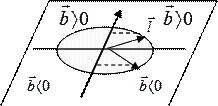
Рисунок 7. Выбор знака вектора Бюргерса
Вектор Бюргерса, в т.ч. и его знак, сохраняется в подвижной системе координат, связанной с осью дислокации 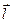, если передвигать контур Бюргерса вдоль криволинейной оси дислокации (рис.8а).
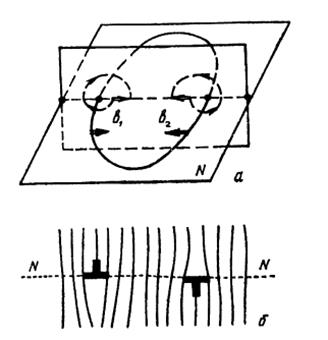
Рис 8 Различие в знаке вектора Бюргерса у противоположных сторон петли дислокации:
а – вид в плоскости скольжения N (разрывы контура Бюргерса направлены навстречу друг другу); б – сечение нормальной к этой плоскости (избыточные полуплоскости лежат по разные стороны о плоскости скольжения N)
В любой неподвижной системе координат, связанной с решеткой, противоположные ветви дислокации имеют разный знак (в двух точках сечения плоскостью одной и той же криволинейной дислокации векторы Бюргерса разноименные). Смена знака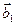 
и 
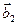связана со сменой знака оси дислокации на противоположный справа (положительный, когда в неподвижной системе координат, связанной с решеткой мы смотрим в «хвост» вектора оси 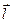) и слева (отрицательный, когда в той же системе координат вектор оси 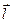«смотрит на нас»).
В сечении (рис. 8б) 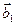и 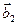имеют разный знак. Это отражает физическое различие двух ветвей дислокации: избыточная полуплоскость от ветви 1 сверху, а от ветви 2 – она снизу.
Смена знака вектора Бюргерса от перемены «положительного» направления оси дислокации, приводит к равенству нулю суммы векторов Бюргерса при движении к одной и той же точке дислокации с противоположных сторон: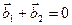 
. Это верно и для всякой точки ветвления дислокаций: 
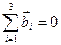, если направления всех дислокаций идут к точке ветвления то, как в законе Кирхгофа для электрических цепей, сумма векторов Бюргерса при движении к одной и той же точке дислокации с противоположных сторон нулевая.
Дислокацию в каждой точке, поэтому характеризуют два независимых вектора: единичный вектор оси 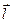и вектор Бюргерса .
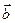Поэтому для количественного описания дислокация является тензорным бесконечно протяженным объектом произвольной конфигурации
Тензор –совокупность трех векторов в данной системе координат, преобразующихся по определенному закону в совокупность других трех векторов, отвечающих другой системе координат.
Дата добавления: 2015-03-20; просмотров: 1423;