Математическое моделирование процесса термоподготовки углей

Процессом термической подготовки углей необходимо управлять. В связи с этим потребовалось создание математической модели температурной обработки частиц угольной пыли [197], в разработке которой принимал непосредственное участие автор настоящих исследований. Поток аэросмеси поступает в камеру термоподготовки, имея начальный объем 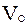и температуру Т. В камере термоподготовки происходит термодеструкция угольной пыли. Для того, чтобы оценить вклад каждого из факторов, влияющих на процесс термоподготовки топлива следует рассмотреть отдельные составляющие теплового баланса элементарного объема пылегазовой струи.

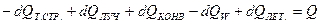, (4.1)

где 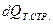– изменение теплосодержания струи, Дж; 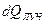– лучистое тепло от облучателя, Дж; 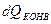– тепло от конвективного обмена между частицей и газом, Дж; 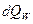– тепло, расходуемое на нагрев влаги, Дж;
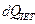– тепло за счёт диффузной теплопроводности от потока летучих, Дж.

Изменение теплосодержания газовой смеси:

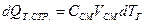(4.2)

где 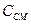– теплоёмкость газовой смеси, Дж/м 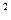K; 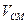– объём газовой смеси, окружающей частицу, м 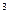; 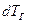– изменение температуры газа за время dt, K.

Тепло, подводимое излучением от облучающей среды:

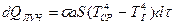, (4.3)

где 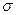– коэффициент излучения абсолютно чёрного тела, Вт/м 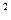K;
a – степень черноты газовой среды; S – поверхность газовой среды, м ;
– температура излучающей среды, K.

Тепло от конвективного обмена между частицей и газом:

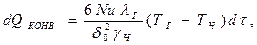(4.4)

где 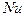– критерий Нуссельта; 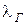– коэффициент теплопроводности газов, Вт/м 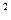k; 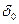– размер частицы, м; 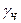– плотность частицы, кг/м ;
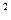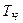– температура частицы, K.

Тепло, расходуемое на нагрев влаги:

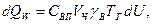(4.5)

где 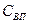– теплоёмкость водяных паров, Дж/кг K; 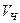– объём частицы, м 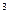; 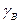– плотность водяных паров в частице, кг/м 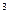; 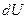– изменение влажности частицы.

Тепло за счёт диффузионной теплопроводности от потока летучих:

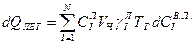, (4.6)

где 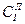– теплоёмкость i-го компонента летучих веществ, Дж/кг K;
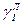– плотность i-го компонента в составе летучих веществ; 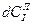– выделение i-го компонента в составе летучих веществ за время 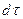, кг/кг.

Из уравнения теплового баланса струи, учитывая изменение отдельных членов, можно определить изменение температуры пылегазовой смеси во времени:

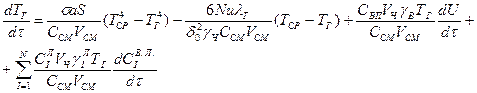(4.7)

Как видно из уравнения (4.7) для определения изменения температуры газов во времени необходимо знать величины температуры частиц – Т , количество выделившихся 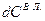летучих веществ, количество испарившейся влаги – .

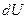Изменение температуры топливных частиц во времени можно определить из рассмотрения теплового баланса частиц в струе:

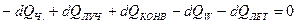, (4.8)

где 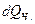– изменение теплосодержания частиц в струе, Дж;
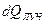– количество тепла, получаемое частицей излучением, Дж; 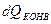– количество тепла, получаемое частицей за счёт конвекции, Дж; 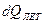– количество тепла, расходуемое на выход летучих веществ, Дж; 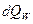– количество тепла, затрачиваемое на выход влаги, Дж.

Изменение теплосодержания частицы запишется

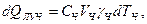(4.9)

где 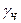– плотность частицы, кг/м 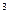; 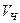– объём частиц, м ;
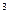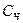– теплоёмкость частицы, Дж/кг*K; 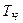– температура частицы, K.

Количество тепла, получаемое излучением:

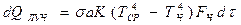(4.10)

где: 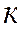– коэффициент облучённости; 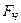– поверхность частицы, м .

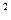Количество тепла, полученное конвекцией:

(4.11)

Тепло, расходуемое на выход летучих веществ:

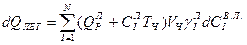, (4.12)

где 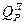– теплота разложения летучих, Дж/кг; 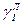– плотность i-го компонента в составе летучих, кг/м 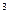; 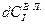– количество i-го компонента в составе летучих, выделившихся из частицы за промежуток времени dt, кг/кг.

Тепло, затрачиваемое на испарение влаги:

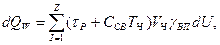(4.13)

где 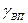– плотность водяных паров в частице, кг/м .

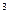Учитывая значение отдельных членов теплового баланса частиц во времени, следует записать:

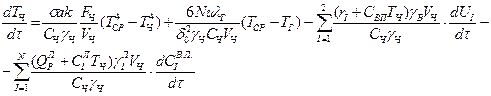(4.14)

Выход летучих можно описать следующей зависимостью:

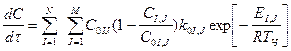, (4.15)

где I – количество продуктов термического разложения в составе выделившихся летучих; J – количество стадий выхода индивидуальных продуктов термического разложения; 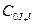– исходная концентрация в топливе i-го компонента разлагающегося на j-ой стадии, кг/кг; 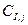– концентрация выделившегося i-ого компонента на j-ой стадии за промежуток времени dt, кг/кг; 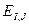– энергия активации выхода i-го компонента в j-ой стадии, Дж/моль; 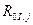– предэкспонента процесса выхода i-ого компонента в j-ой стадии, I/с; 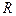– универсальная газовая постоянная, Дж/моль K.

Количество испарившейся влаги можно определить из следующего уравнения:

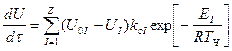кг/кг ºс, (4.16)

На рисунках 4.1 – 4.2 представлены результаты расчета температуры частицы и газовой среды, изменения влажности и выхода летучих веществ при термической обработке березовского угля разной степени окисленности частиц размером 100, 200, 500, 1000 мкм, при начальной температуре газовой среды Т 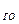= 1000 °С.

1200

Тг, Тr,

C^o

1 2 3

Тг

Тr

W^h, W^св,

C_co2, C_cн4, 1 2 3 W^h

C_cм, C_co+н2, W^св

% C_co2

C_cм

C_cн4

60 C_co+н2

1 2 3 4 5 τ, сек 7

Рисунок 4.1 – Результаты численного эксперимента по моделированию процесса термической подготовки рядового березовского угля Т_го = 1273°К

1 – δ₄₀ = 200 мкм; 2 – δ₄₀ = 500 мкм; 3 – δ₄₀ = 1000 мкм

Анализ результатов численного моделирования показывает, что процесс термической подготовки угля представляет собой совокупность двух последовательных температурных стадий. Первая стадия характеризуется неизотермичностью процесса термообработки. На второй стадии протекают процессы деструкции угля при постоянной температуре.

1200

Тг, Тr,

C^o 1 2 3

W^h, W^св, 1 2 3

C_co2, C_cн4,

C_cм, C_co+н2,

%

1 2 3 4 5 τ,сек 7

Рисунок 4.2 –Результаты численного эксперимента по моделированию процесса термической подготовки рядового березовского угля Т_го = 1273°К

Причем, длительность первой стадии и температура второй Т 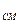во многом определяются не только начальной температурой газов Т 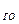, но и размером частиц, подвергающихся термической переработке и степенью окисленности исходного угля.

На рис. 4.3 представлено изменение температуры прогрева частиц Т 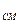от начальной температуры газов Т 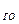, и степени окисленности. При увеличении крупных частиц Т 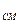имеет тенденцию снижаться, а изменение практически не зависит от начальной температуры газов. Для частиц одной и той же крупности температура Т 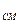при термообработке рядового березовского угля выше, чем окисленного и сажистого, что объясняется значительно большим содержанием влаги и балластных летучих у сажистых и окисленных углей по сравнению с рядовыми. С увеличением крупности частиц влияние степени окисленности на 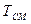возрастает. Так, если для частиц 200 мкм при термоподготовке рядового березовского угля 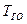=600 ºС величина 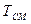составляет 450°С, а сажистого 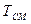= 425°С, то для частиц 1000 мкм 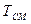соответственно для рядового составляет 350 ºС, а сажистого уже 260°С. При повышении начальной температуры газов 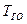влияние роста степени окисленности исходного березовского угля на 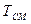усиливается, что, по нашему мнению, обусловлено особенностями кинетики выхода, как балластных, так и теплоценных летучих. Как показал численный эксперимент, это справедливо для всех размеров монофракций угольных частиц.

Различие по степени окисленности исходного березовского угля наряду с крупностью частиц 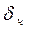, обуславливает продолжительность ( 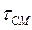) неизотермической стадии термообработки угольных частиц. Для частиц с размером 200 мкм при термообработке рядового березовского угля 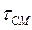составляет 0,8 с, окисленного 1,5 с; для 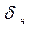=500 мкм, 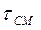=2,2 с; 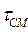= 4,1 с, соответственно, при обработке рядового и окисленного угля. Для частиц 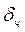= 1000 мкм 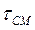рядового угля составила 8,1 с, окисленного 14,5 с.

Значительная величина длительности иеизотермической стадии соизмерима с величиной времени термической обработки пылеугольных частиц в реальных технологических условиях. Этот факт позволяет сделать вывод о существенной неизотермичности процесса термической подготовки твердых топлив перед сжиганием.

1000

T_см 1 2 3

200 400 600 d_r, мкм 1000

Рисунок 4.3-Изменение температуры прогрева пылеугольных частиц
в зависимости от их размера и начальной температуры газов

∆ - рядовой уголь; o – окисленный; - сажистый

1-Т=1273 К; 2-Т=1073 К; 3-Т=873 К

В результате аналитических исследований установлено существенное влияние степени окисленности березовского yгля на температурно-временную зависимость ( 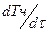) обработки пылеугольных частиц, что необходимо учитывать при разработке режимов термической подготовки канско-ачинских углей

Система уравнений(4.7, 4.14, 4.15, 4.16) была решена методом Рунге–Кутта–Фельдберга. При этом выполнены следующие условия: полное удаление из угольной частицы влаги и балластных летучих веществ; обеспечение стабильного воспламенения топливных частиц при минимальной концентрации в них летучих веществ; отсутствие неполноты сгорания топлива.

Решение системы уравнений (4.7, 4.14, 4.15, 4.16) с учетом выбранных условий позволило определить необходимый режим термоподготовки КАУ, а именно: при времени термообработки угольных частиц 0,8–1,2 с рекомендуемая температура обработки для рядового березовского угля при крупности помола, принятой для КАУ на ТЭС, составляет 460–480 ^оС, для окисленного угля –580–610 ^оС, для сажистого угля – 630–650 ^оС. Полученные результаты численного моделирования хорошо согласуются с экспериментальными исследованиями.