Графические методы

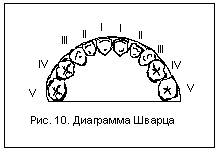1. Диаграмма Schwarz применяется для оценки формы зубных рядов во временном прикусе. В основу построения диаграммы положено представление о том, что форма зубных дуг во временном прикусе приближается к полуокружности (рис. 10).

Методика построения диаграммы:

1. Измеряют расстояние между дистально-щечными бугорками вторых временных моляров, которое будет являться в последующем диаметром полуокружности.

2. Далее на полученную полуокружность прикладывают модель и обводят контур по зубам. Полученный результат сравнивают с нормой.

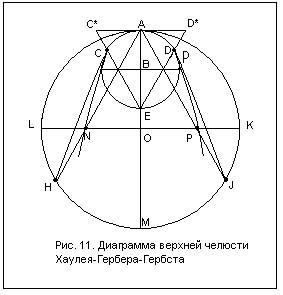2. Диаграмма Hawley–Herber–Herbst, как и диаграмма Шварца, применяется для оценки формы зубных рядов, но только в постоянном прикусе. Hawley предложил диаграмму в 1904 году, а Herber иHerbst в 1907. Диаграмма основана на антропометрической зависимости величины и формы зубной дуги от суммы Мd размеров коронок верхних фронтальных зубов (центрального и бокового резцов и клыка) (рис. 11).

Методика построения диаграммы:

1. Измеряют Мd размеры коронок центрального, бокового резцов и клыка на одной стороне, суммировав данные, получают радиус (малый – r) АВ, которым из точки В описывается малая окружность.

2. На окружности из точки А малым радиусом откладывают отрезки АС и АD. Кривая САDпредставляет собой кривуюрасположения шести фронтальных зубов.

3. Из точки Е проводят прямые через точки С и D соответственно до пересечения с касательной к точке А, в результате чего получают равносторонний треугольник ЕC*D*(т.е. EC*= CD*= ED*).

4. Радиусом, равным стороне этого треугольника (большим – R), из точки А на продолжении оси ординат отмечают точку О – центр большой окружности, из которой описывают окружность.

5. Из точки М большим радиусом откладывают точки J и H.

6. Соединив точки J с D и H с С, получают кривую НСАDJ, которая является кривой всей верхней зубной дуги (по Hawley).

7. Herbst соединил точки Н с А и J с А. На пересечении с горизонтальным диаметром большой окружности получают точки N и P, описывают кривую NСАDР, которая является кривой правильно сформированного верхнего зубного ряда по Hawley–Herber–Herbst.

Для вычерчивания правильной кривой нижней челюсти рекомендуется первоначальный радиус брать на 2 мм меньше (по мнению Hawley). Кроме того, на кривой САD располагаются не только резцы и клыки, но и первые премоляры.

Для определения соответствия формы зубного ряда данного пациента диагностическую модель прикладывают к чертежу так, чтобы средняя линия, проходящая по небному шву, совпадала с осью ординат, а стороны равностороннего треугольника проходили между клыками и премолярами.

С целью облегчения работы врача-ортодонта на кафедре стоматологии детского возраста ИГМУ разработаны шаблоны диаграмм Schwarz и Hawley–Herber–Herbst соответственно с разными Мd размерами зубов необходимыми для данных диаграмм, что дает возможность подобрать для каждого случая соответствующую диаграмму и сравнить с диагностической моделью пациента. Использование данных шаблонов облегчает применение диаграмм в практической работе врача-ортодонта.

Тестовые задания:

1. Для определения размеров апикального базиса челюсти используют

1) метод Пона

2) метод Хауса–Снагиной

3) индекс Тона

1. Длину переднего отрезка определяют с помощью методов

1) Пона

2) Коркхауза

3) Хауса–Снагиной

1. Индекс Тона применяют для определения

1) пропорциональности размеров верхнего и нижнего зубных рядов

2) ширины зубного ряда

3) пропорциональности размеров верхних и нижних резцов

1. Метод Герлаха применяют для определения

1) длины тела нижней челюсти

2) ширины зубного ряда

3) пропорциональности размеров боковых и передних сегментов зубных рядов верхней и нижней челюстей

1. Графический метод Хаулея–Гербера–Гербста применяют для определения нарушения

1) длины зубных рядов

2) ширины зубных рядов

3) положения зубов и формы зубных рядов

1. Пропорциональность размеров коронок постоянных резцов верхней и нижней челюстей позволит определить

1) метод Пона

2) метод Коркхауза

3) индекс Тона

1. Метод Пона основан

1) на зависимости суммы мезиодистальных размеров 4 нижних резцов и ширины зубного ряда в переднем и заднем отделах

2) на зависимости суммы мезиодистальных размеров верхних резцов и ширины зубных рядов

3) на пропорциональности размеров 4 верхних и 4 нижних резцов

1. Размеры зубных рядов по методу Пона изучаются

1) в сагиттальном направлении

2) в сагиттальном и вертикальном направлениях

3) в трансверзальном направлении

1. Индекс Тона в норме равен

1) 1,35

2) 1,22

3) 1,5

1. Премолярный индекс Пона равен

1) 80

2) 85

3) 64

1. Метод Коркхауза основан

1) на пропорциональности трансверзальных и сагиттальных размеров зубов

2) на зависимости суммы мезио-дистальных размеров 4 верхних резцов и длины переднего отрезка зубного ряда

3) на отношении ширины и длины зубных рядов

1. Данные, полученные при измерении гипсовых моделей челюстей по методу Герлаха, свидетельствуют

1) об изменении ширины и длины зубных рядов

2) о соотношении размеров боковых сегментов зубных рядов

3) о соотношении фронтального и боковых сегментов зубных рядов

1. Молярный индекс Пона равен

1) 80

2) 85

3) 64

1. Методика Хауса–Снагиной позволяет определить

1) форму зубных рядов

2) степень развития базиса

3) размеры сегментов зубных рядов

1. Для определения нарушения формы зубных рядов используют методики

1) Пона

2) Коркхауза

3) Хаулея–Гербера–Гербста

1. Диаграмма Хаулея–Гербера–Гербста позволяет определить

1) размеры зубных рядов

2) форму зубных рядов

3) размеры сегментов зубных рядов