Если (5.4) подвергнуть преобразованию Фурье, то получим

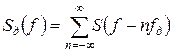, (5.5)

где S(f)и S_д(f) – спектры исходной и дискретизированной функций соот­­ветственно [11].

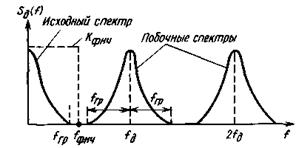
Из (5.5) следует, что спектр дискретизированного сигнала представляет собой сумму исходного спектра (п=0) и «побочных» или дополнительных спектров того же вида, но сдвинутых один относительно другого на f_д, 2f_д и т. д. (рис.5.3). Из рисунка видно, что с помощью идеального фильтра нижних частот (ФНЧ) с частотой среза f_ФНЧ можно выделить спектр исходного сигнала, если выполняются два условия:

f_д ³ 2 f_гр и f_гр £ f_ФНЧ £ f_д – f_гр .

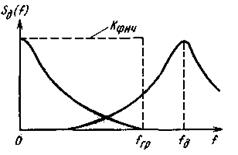
Если же частота отсчетов выбрана из условия f_д < f_гр, то после дискретизации побочные спектры будут перекрывать основной, и в общем виде восстановить исходный сигнал без помех (рис. 5.4) невозможно. Однако к настоящему времени разработаны такие методы дискретизации ТВ сигнала, которые позволяют и в этом случае восстановления исходного сигнала избавиться от побочных продуктов.

Рис. 5.3. Спектр сигнала после дискретизации	Рис. 5.4. Перекрытие спектров при fд < 2 fгр

Значимость этих методов сегодня очень велика, поскольку возможное
снижение частоты дискретизации позволяет пропорционально уменьшить цифровой поток, т.е. сделать систему цифрового телевидения более экономичной.

Прежде чем рассмотреть эти методы, следует указать на то, что при кодировании телевизионного сигнала чаще всего применяется дискретизация с постоянной частотой. В свою очередь, частота дискретизации может быть связана или не связана с частотой строчной и кадровой разверток. При жесткой связи получается постоянное число отсчетов в строке, соответствующих одним и тем же элементам изображения. На изображении при этом образуется фиксированная структура отсчетов (структура дискретизации).

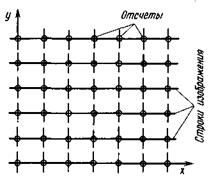
Ортогональная структура дискретизации. Если частоту отсчетов в сигнале выбрать кратной частоте строк, то на изображении будет образована ортогональная структура дискретизации, в которой отсчеты располагаются в узлах прямоугольной решетки (рис.5.5).

В цифровых устройствах ТВ вещания этот способ дискретизации в настоящее время является наиболее распространенным. Если принять частоту дискретизации f_д = 2 f_гр, то число отсчетов в изображении будет равно числу его условных телевизионных элементов, составляющих около 300 тыс. Попытаться сократить число отсчетов – значит пропорционально уменьшить разрешающую способность ТВ системы и соответственно ухудшить качество изображения. Это рассуждение предполагает, что наш зрительный аппарат воспринимает изображение как хаотическое распределение различных яркостей в структуре отсчетов и анализирует это изображение точка за точкой. На самом деле это не так. В изображениях существуют значительные статистические связи, к которым в результате эволюционного развития приспособился наш зрительный аппарат. В частности, установлено [11], что зрительный анализатор содержит совокупности рецепторов (рецептивные поля), кодирующие одновременно большие группы элементов изображения, реагируя при этом не столько на их яркость, сколько на форму, выделяя из фона изображения наиболее его информативную часть: контуры, перепады яркости. Важно заметить, что такие свойства зрительного аппарата позволяют ему восстановить целостные контуры даже при их распаде на отдельные элементы вследствие дискретизации или из-за действия случайных помех.

Эти свойства зрительного анализатора позволяют допустить, что в ТВ системе не обязательно обеспечивать условия для передачи каждого из элементов изображения. Можно удовлетвориться передачей определенного ансамбля конфигураций, при этом с пониженным (по отношению к стандартному) числом элементов.

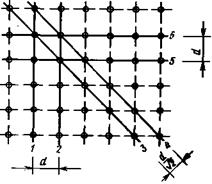
Оценим с таких позиций возможности ортогональной структуры отсчетов при получении изображения. Для этого нанесем на ней самые элементарные конфигурации: вертикальные, горизонтальные и наклонные линии, представляющие собой детали некоего ТВ изображения (рис.5.6).

Рис. 5.5. Ортогональная структура дискретизации	Рис. 5.6. К определению разрешающей способности системы с ортогональной структурой дискретизации

Условимся, что минимальное расстояние между соседними контурами, расположенными по вертикали или горизонтали (линии 1 и 2 или 5 и 6 на рис.5.6), равно шагу дискретизации – расстоянию между соседними отсчетами. Из рисунка видно, что наклонные контуры, ориентированные по диагонали (линии 3, 4)содержат меньшее число элементов на одном и том же участке по сравнению с вертикальными и горизонтальными линиями. Тем не менее, глаз благодаря развитой системе нейронов их объединяет в общие диагональные линии. Эти линии не распадаются на отдельные элементы, а воспринимаются слитно. Обратим внимание также на следующее. При орто­гональной структуре отсчетов расстояние между наклонными линиями мень­ше, чем между вертикальными и горизонтальными в 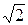раз, т.е. ортогональная структура отсчетов обеспечивает в диагональных направлениях большую разрешающую способность по сравнению с горизонтальным и вертикальным направлениями. В этом обнаруживается несовершенство ортогональной структуры дискретизации. Известно, что разрешающая способность зрения анизотропна, т.е. неодинакова в различных направлениях. Она максимальна вдоль вертикальной и, горизонтальной осей, примерно в 1,5 раза превышая разрешающую способность в диагональных направлениях. В этом проявляется адаптация зрения к статистике изображений, в которых преобладают перепады яркости в вертикальных и горизонтальных направлениях.

Таким образом, ортогональная структура дискретизации изображения с шагом дискретизации, удовлетворяющим условиям теоремы Котельникова, характеризуется заметной избыточностью в разрешающей способности системы по диагональным направлениям. Устранять эту избыточность путем уменьшения числа отсчетов (т.е. уменьшая частоту дискретизации) нельзя, так как при этом ухудшится четкость изображения в самых важных направлениях по горизонтали и вертикали.

Рассмотрим другую, более совершенную с этих позиций структуру дискретизации.

Шахматная структура дискретизации. Зададимся, как и в предыдущем случае, числом отсчетов в изображении, соответствующим частоте дискретизации f_д = 2f_гр. Тогда каждому элементу изображения, как и раньше, будет соответствовать определенный отсчет. Если расположить эти отсчеты таким образом, чтобы в соседних строках они были смещены друг относительно друга на половину шага дискретизации (половину размера одного элемента изображения) d/2, то будет образована структура отсчетов, называемая шахматной (рис.5.7). Нанесем на этой структуре простейшие конфигурации изображения из горизонтальных, вертикальных и наклонных линий. Оценим качество их воспроизведения и минимально возможные расстояния между ними.

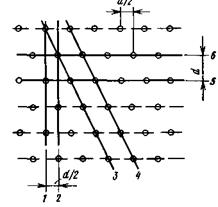
Рис. 5.7. К определению разрешающей способности системы с шахматной структурой дискретизации

Горизонтальные линии 5 и 6 воспроизводятся, как и при ортогональной структуре дискретизации, с той же детальностью, т.е. состоят из такого же числа отдельных элементов изображения. Минимальное расстояние между ними также не изменилось. Оно равно расстоянию между соседними строками, т.е. шагу дискретизации d. Таким образом, разрешающая способность системы в вертикальном направлении сохранилась прежней.

Вертикальные линии 1 и 2 воспроизводятся теперь в виде более грубой структуры, содержащей в 2 раза меньшее число элементов. Однако, как показывает эксперимент, зрительно на качестве воспроизведения вертикальных контуров это почти не сказывается. Зато очень существенно увеличилась разрешающая способность системы по горизонтали. Она характеризуется при шахматной структуре дискретизации в 2 раза меньшим расстоянием между двумя соседними вертикальными линиями d/2. В диагональных направлениях (линии 3 и 4) интервалы между контурами примерно в 1,8 раза больше, чем в горизонтальном направлении. Но именно в этих направлениях существенно ниже и разрешающая способность зрения (рис.5.8). То есть ортогональная структура отсчётов ухудшает разрешение в наиболее важных для зрения направлениях – по вертикали и горизонтали. Шахматная структура дискретизации оказывается лучше согласована с особенностями зрительного аппарата и позволяет за счет понижения разрешающей способности в направлениях, где это не скажется заметно на восприятии, понизить общее число отсчетов в кадре, т.е. уменьшить частоту дискретизации.

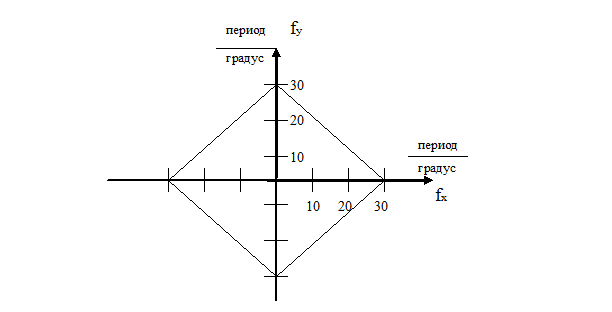
Рис.5.8 Пространственная разрешающая характеристика зрительного анализатора человека

Напомним, что уменьшение частоты дискретизации ниже 2 f_гр приводит к перекрытию основного и побочного спектров дискретного сигнала (см. рис.5.4), а значит, к невозможности в общем случае безыскаженного восстановления исходного сигнала. Однако шахматная структура дискретизации при определенных условиях позволяет в значительной степени избавиться от помех, связанных с перекрытием основного и побочного спектров.

Чтобы понять механизм устранения помех при перекрытии спектров в шахматной структуре отсчетов, напомним, что спектр ТВ сигнала состоит из гармоник, кратных частоте строк, около которых группируются узкие полосы боковых частот, обусловленные кадровой разверткой и перемещением деталей изображения. На участке спектра соответствующих гармоник строчной частоты сосредоточены максимумы энергии сигнала, а посередине между ними – минимумы. В зависимости от содержания изображения отношение максимума к минимуму лежит в пределах 2...35 дБ. Аналогичную структуру имеет спектр и побочных продуктов дискретизации. Поэтому если частота дискретизации ТВ сигнала кратна полустрочной частоте, то энергия мешающих составляющих сосредоточивается в зоне минимума энергии исходного сигнала. На рис.5.9 сплошными линиями показано распределение максимумов энергии сигнала основного спектра, а штриховыми – побочного. С помощью гребенчатого фильтра удаляются мешающие составляющие в диапазоне от (f_д – f_гр) до f_гр. Гребенчатый фильтр должен быть рассчитан таким образом, чтобы иметь максимальное затухание на мешающих частотах и минимальное затухание на частотах полезных составляющих.

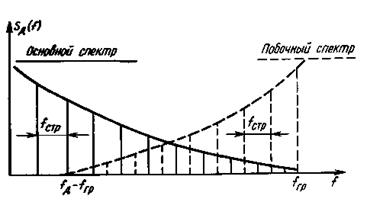
Рис. 5.9. Перекрытие основного и побочного спектров

при шахматной структуре дискретизации

При ортогональной дискретизации максимумы энергии составляющих основного и побочного спектров накладываются друг на друга, что делает невозможным разделение их с помощью гребенчатого фильтра.

Таким образом, шахматная структура дискретизации отсчетов позволяет без существенного ущерба качеству изображения снизить минимально допустимую частоту дискретизации с 12 МГц (при ортогональной структуре) до 8...8,5 МГц и соответственно пропорционально уменьшить цифровой поток ТВ сигнала. В этом ее главное достоинство.

Шахматная структура дискретизации, конечно, не свободна от помех, которые могут проявляться в виде зазубренности границ перепадов яркости и муаров. Однако в настоящее время разработаны способы временной и пространственной фильтрации, сводящие эти помехи к минимуму.