Параметрические измерительные преобразователи неэлектрических величин

Измерительные преобразователи неэлектрических величин делятся на параметрические и генераторные. В параметрических преобразователях выходной величиной является приращение параметра электрической цепи (R, L, М, С), поэтому при их использовании необходим дополнительный источник питания.

В генераторных преобразователях выходной величиной являются ЭДС, ток или заряд которых функционально связанные с измеряемой неэлектрической величиной.

При создании измерительных преобразователей неэлектрических величин стремятся получить линейную функцию преобразования. Отличие реальной градуировочной характеристики от номинальной линейной функции преобразования обусловливает погрешность нелинейности, являющуюся одной из главных составляющих результирующей погрешности при измерениях неэлектрических величин. Одним из способов снижения погрешности нелинейности является выбор в качестве входных и выходных величин преобразователя таких величин, взаимосвязь которых ближе к линейной функции. Так, например, при измерении линейных перемещений с помощью емкостного преобразователя может изменяться либо зазор между пластинами, либо площадь их перекрытия. При этом функции преобразования оказываются различными. При изменении зазора зависимость емкости от перемещения подвижной пластины существенно нелинейная, она описывается гиперболической функцией. Однако, если в качестве выходной величины преобразователя использовать не его емкость, а сопротивление на некоторой частоте, то измеряемое перемещение и указанное емкостное сопротивление оказываются связанными линейной зависимостью.

Другим эффективным способом уменьшения погрешности нелинейности параметрических измерительных преобразователей является их дифференциальное построение. Любой дифференциальный измерительный преобразователь фактически представляет собой два аналогичных измерительных преобразователя, выходные величины которых вычитаются, а входная величина воздействует на эти преобразователи противоположным образом.

Структурная схема прибора с дифференциальным измерительным преобразователем приведена на рисунке 16.1.

Измеряемая величина х воздействует на два аналогичных измерительных преобразователя ИП1 и ИП2, причем соответствующие приращения значений выходных величин у₁ и у₂ имеют противоположные знаки. Кроме того, есть некоторое постоянное начальное значение x₀ величины

на входах этих преобразователей, определяемое обычно конструктивными параметрами преобразователей. Выходные величины у₁ и у₂ вычитаются, а их разность у₃ измеряется электроизмерительным устройством ЭИУ (аналоговым или цифровым).

Предположим, что преобразователи ИП1 и ИП2 идентичны, а их функции преобразования достаточно точно описываются алгебраическим полиномом второго порядка. В этом случае значения у₁ и у₂ на выходах преобразователей можно записать виде (16.1) /14/

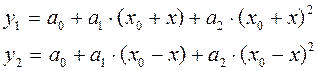, (16.1)

После вычитания получим (16.2) /14/

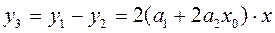, (16.2)

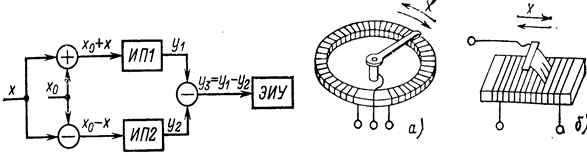
Рисунок 16.1 - Структурная схема диф- Рисунок 16.2 - Реостатные из- ференциального измерительного пре- мерительные преобразователи

образователя

Отсюда видно, что результирующая функция преобразования y₃ = f(х) оказалась линейной. Так как у₃ не зависит от а₀ , то происходит компенсация систематических аддитивных погрешностей измерительных преобразователей. Кроме того, по сравнению с одним преобразователем практически вдвое возрастает чувствительность. Все это определяет широкое применение дифференциальных измерительных преобразователей в практике.

Рассмотрим кратко основные типы используемых параметрических преобразователей неэлектрических величин.