Глава IV.СВОБОДНЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНОЙ КОНСЕРВАТИВНОЙ СИСТЕМЕ

Напомним, что консервативной системой называется такая колебательная система, энергия которой сохраняется неизменной. В действительности таких систем нет, но если время наблюдения невелико, потери энергии за это время пренебрежимо малы, то представление реальной системы консервативной вполне оправдано. В ряде случаев математический анализ консервативных систем значительно проще. Если система к тому же линейная, то результаты могут быть получены в аналитической форме. Для нелинейных систем не всегда возможно получить решения уравнений. Однако качественный анализ консервативной системы с любой нелинейностью может быть проведен методом фазовой плоскости. Последнее утверждение основано на том, что для консервативных систем всегда существует интеграл энергии

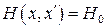, (4.1)

где .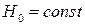

В случае механической системы полная энергия есть сумма кинетической 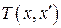и потенциальной 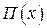энергий

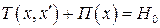, (4.2)

в электрической системе полная энергия есть сумма электрической и магнитной энергии

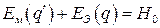. (4.3)

Если даны динамические уравнения, то можно получить выражения, в явном виде связывающие и .

Рассмотрим механическую систему: груз, подвешенный к пружине (Рис.30).

В общем случае сила упругости является нелинейной функцией смещения, и динамическое уравнение имеет вид;

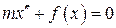, (4.4)

где 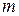– масса, 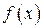- сила пружины.

Перейдем к уравнению на фазовой плоскости. Запишем два уравнения первого порядка

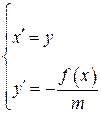. (4.5)

Исключаем время

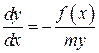. (4.6)

В уравнении переменные разделяются

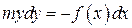. (4.7)

Интегрируя, получаем интеграл энергии

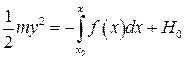. (4.8)

Где 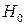- постоянная, зависящая от начальных условий.

По определению

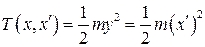- кинетическая энергия,

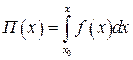- потенциальная энергия.

Уравнение (4.8) представляет условие консервативности системы (4.2)

Электрическим аналогом рассмотренной механической системы может служить контур с нелинейной емкостью (Рис.31).

Уравнение контура

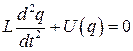, (4.9)

где 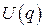- вольт - кулоновская характеристика нелинейной емкости.

Переходя, к уравнению на фазовой плоскости, получим

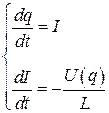. (4.10)

Исключив время получим

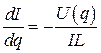. (4.11)

Разделяем переменные

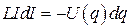. (4.12)

Интегрируем и получаем интеграл энергии (4.3)

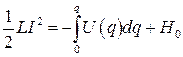, (4.13)

Очевидно:

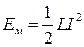- магнитная энергия, запасенная индуктивностью,

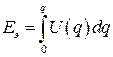- энергия, запасенная емкостью.

В общем случае интеграл энергии (4.1) представляет уравнение фазовой траектории в виде неявной функции. В частности, в часто встречающемся случае, когда кинетическая (или магнитная) энергия имеет вид

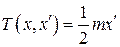. (4.14)

Можно записать уравнение фазовой траектории в виде явной функции:

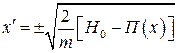. (4.15)

Знак 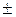означает, что фазовой портрет симметричен относительно оси координат. Эта формула лежит в основе графического способа построения фазового портрета.

Исходным является график зависимости потенциальной энергии от координаты. Остальные процедуры выполняются согласно формуле (4.15) (из 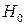вычитается 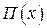, извлекается квадратный корень, умножается на постоянный множитель).

Проанализируем свободные колебания математического маятника методом фазовой плоскости. Проведем графического построение фазового портрета математического маятника (Рис.32)

Кинетическая энергия маятника

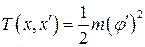. (4.16)

Это выражение совпадает по форме с (4.14). Формула, аналогичная (4.15), имеет вид:

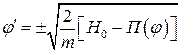(4.17)

Потенциальную энергию, как функцию угла, легко найти аналитически, используя рисунок 32.

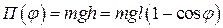. (4.18)

Для построения фазового портрета математического маятника используем график 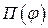(Рис.33). Порядок построения следующий.

-Задаем начальную энергию 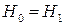и на графике для потенциальной энергии проводим прямую 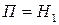. Точкам пересечения 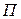и 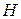на фазовой плоскости соответствует координаты с нулевой скоростью.

-Затем берутся разностим 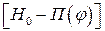, которые на графике выделены утолщенными отрезками.

-Извлекается корень и соответствующее 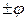наноситься на нижнем графике. (Множитель 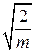является масштабным и может быть учтен при нанесении шкалы по оси ).

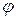-По точкам строится кривая .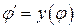

-Затем берется другое начальное значение 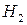и все операции повторяются.

Аналогично получаем соответствующие траектории для различных значений потенциальных энергий 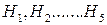. После этого стрелками указываем направление движения изображающей точки.

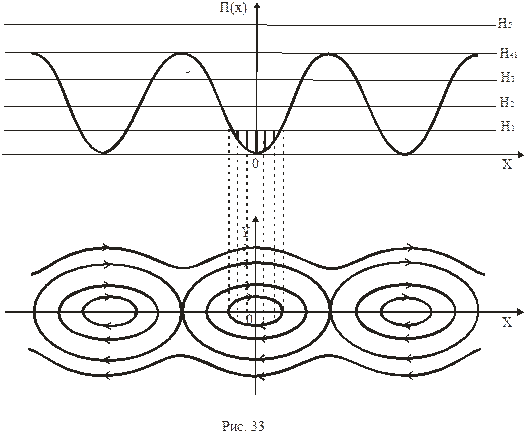
Проанализируем фазовый портрет.

1) Особые точки соответствуют экстремумам потенциальной энергии: центры минимумам, седла максимумам.

2) При малых углах отклонения фазовые траектории близки к эллипсам (колебания гармонические).

3) При больших углах отклонения (больших начальных энергиях 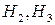) фазовые траектории замкнуты, но отличаются от эллипсов (колебания негармонические).

4) Траектория 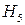не замкнута и соответствует тому, что маятник вращается – угол все время нарастает, меняется величина угловой скорости, но знак (направления вращения) сохраняется.

5) По траектории 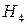невозможно сказать, вращается маятник или колеблется. Эта кривая разбивает фазовую плоскость на области с разным типом движения: области с замкнутыми траекториями, которым соответствует колебательное движение, вне них траектория периодична по 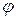- движение вращательное. Фазовая траектория, которая разделяет фазовую плоскость на области с разными типами движения, называется сепаратрисой.

Признаком того, что фазовая кривая может быть сепаратрисой, является прохождение ее через особую точку типа седло. По этой причине при анализе систем, прежде всего определяют положение особых точек типа седло и строят сепаратрисы.

В заключение рассмотрения собственных колебаний в консервативной системе остановимся на возможности отыскания точного аналитического решения.

Необходимыми условиями являются представление фазовой траектории в явном виде (4.18, 4.19) и задание потенциальной энергии 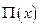в аналитической форме. Выражение

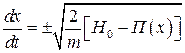. (4.18)

Представляет уравнение первого порядка. Разделяя переменные

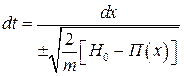(4.19)

и интегрируя

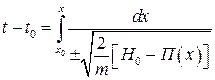, (4.20)

получаем функцию, обратную .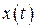

Аналитическое вычисление интеграла в большинстве случаев не удается провести до конца. А в тех случаях, когда это возможно, результат представлен в виде специальных функций. В частности, вычисление интеграла для математического маятника привело к появлению класса эллиптических функций.

Для периодических колебаний формула (4.20) позволяет найти период. С учетом симметрии фазовой траектории период можно найти по следующей формуле:

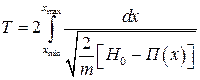. (4.21)

Только в случае линейной системы период колебаний 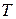не зависит от энергии системы (система изохронная). В общем случае период есть функция энергии 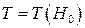- система неизохронная.