Нормальное распределение. Мы уже знакомы с понятиями «распределение», «полигон» (или «частный полигон») и «кривая распределения»

Мы уже знакомы с понятиями «распределение», «полигон» (или «частный полигон») и «кривая распределения». Частным случаем этих понятий является «нормальное распределение» и «нормальная кривая». Но этот частный вариант очень важен при анализе любых научных данных, в том числе и психологических. Дело в том, что нормальное распределение, изображаемое графически нормальной кривой, есть идеальное, редко встречающееся в объективной действительности распределение. Но его использование многократно облегчает и упрощает обработку и объяснение получаемых в натуре данных. Более того, только для нормального распределения приведенные коэффициенты корреляции имеют истолкование в качестве меры тесноты связи, в других случаях они такой функции не несут, а их вычисление приводит к труднообъяснимым парадоксам.

В научных исследованиях обычно принимается допущение онормальности распределения реальных данных и на этом основании производится их обработка, после чего уточняется и указывается, насколько реальное распределение отличается от нормального, для чего существует ряд специальных статистических приемов. Как правило, это допущение вполне приемлемо, так как большинство психических явлений и их характеристик имеют распределения, очень близкие к нормальному.

Так что же такое нормальное распределение и каковы его особенности, привлекающие ученых? Нормальным называется такое распределение величины, при котором вероятность ее появления и не появления является одинаковой. Классическая иллюстрация – бросание монеты. Если монета правильна и броски выполняются одинаково, то выпадение «орла» или «решки» равновероятно. То есть «орел» с одинаковой вероятностью может выпасть и не выпасть, то же касается и «решки».

Мы ввели понятие «вероятность». Уточним его. Вероятность– это ожидаемая частота наступления события (появления – не появления величины). Выражается вероятность через дробь, в числителе которой – число сбывшихся событий (частота), а взнаменателе – предельно возможное число этих событий. Когда выборка (число возможных случаев) ограниченна, то лучше говорить не о вероятности, а очастости, с которой мы уже знакомы. Вероятность предполагает бесконечное число проб. Но на практике эта тонкость часто игнорируется.

Пристальный интерес математиков к теории вероятности вцелом и к нормальному распределению в частности появляется вXVII веке в связи со стремлением участников азартных игр найти формулу максимального выигрыша при минимальном риске. Этими вопросами занялись знаменитые математики Я. Бернулли (1654-1705) и П. С. Лаплас (1749-1827). Первым математическое описание кривой, соединяющей отрезки диаграммы распределения вероятностей выпадения «орлов» при многократном бросании монет, дал Абрахам де Муавр(1667-1754). Эта кривая очень близка к нормальной кривой,точное описание которой дал великий математик К. Ф. Гаусс(1777-1855), чье имя она и носит поныне. График и формула нормальной (Гауссовой) кривой выглядит следующим образом.

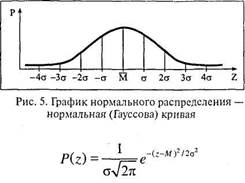
где Р – вероятность (точнее, плотность вероятности), т. е. высота кривой над заданным значением Z; е – основание натурального логарифма (2.718...); π= 3.142...; М – среднее выборки; σ – стандартное отклонение.

Свойства нормальной кривой

1. Среднее (М), мода (Мо) и медиана (Me) совпадают.

2. Симметричность относительно среднего М.

3. Однозначно определяется всего лишь двумя параметрами – М и о.

4. «Ветви» кривой никогда не пересекают абсциссу Z, асимптотически к ней приближаясь.

5. При М = 0 и о =1 получаем единичную нормальную кривую, так как площадь под ней равна 1.

6. Для единичной кривой: Р_м = 0.3989, а площадь под кривой в диапазоне:

-σ до +σ = 68.26%; -2σ до + 2σ = 95.46%; -Зσ до + Зσ = 99.74%.

7. Для неединичных нормальных кривых (М ≠0, σ ≠1) закономерность по площадям сохраняется. Разница – в сотых долях.

Вариации нормального распределения

Представленные ниже вариации относятся не только к нормальному распределению, но к любому. Однако для наглядности мы их приводим здесь.

1. Асимметрия – неодинаковость распределения относительно центрального значения.

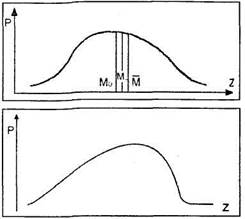
Рис. 6. Графики асимметричного распределения

Асимметрия – третий показатель, описывающий распределение наряду с мерами центральной тенденции и изменчивостью. Эксцесс – показатель, характеризующий скорость нарастания концентрации данных к центральному значению. На графиках это выражается «островершинностью» или «плосковершинностью».

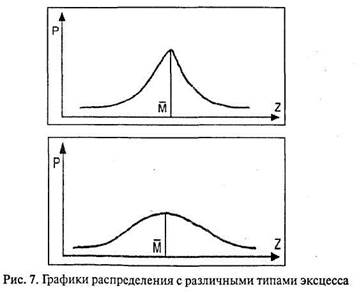
Эксцесс – четвертый основной показатель распределения. 3. Бимодальность– распределение с двумя классами данных в выборке. Об этом эффекте уже говорилось при рассмотрении моды (Мо). На графике это выражается «двувершинностью».