Показатели безотказности невосстанавливаемых объектов
Вероятность безотказной работы P(t) – вероятность того, что в пределах заданной наработки t отказ объекта не возникает,
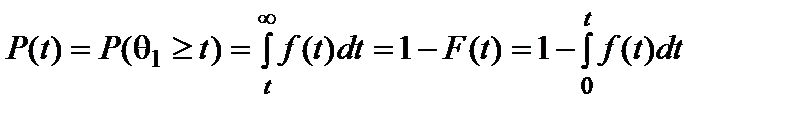 , (6)
, (6)
где θ1 – наработка объекта до отказа (непрерывная случайная величина); f (t) – функция плотности распределения случайной величины θ1; F(t) – вероятность отказа (интегральная функция распределения случайной величины θ1):
 ; t > 0. (7)
; t > 0. (7)
Откуда следует, что 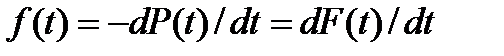 . (8)
. (8)
Поскольку случайная величина наработки всегда положительна, плотность ее распределения обладает следующими свойствами:
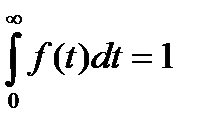 – условие нормировки;
– условие нормировки; 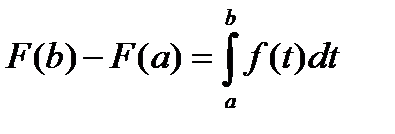 ;
;
| f(t) |
| Рис. 3. Графическая интерпретация вероятностей F(t)и P(t) |
| P(t) |
| F(t) |
| f(t)dt |
| 0t t+∆t →∞ |
| P(t),F(t) |
| 1,0 |
| 0 Meθ1 t |
| 0,5 |
| F(t) |
| P(t) |
| Рис. 4. Графики изменений во времени вероятностей F(t)и P(t) |
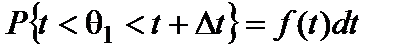 .
.
Эти свойства наглядно иллюстрируют графики на рис. 3 и 4. С ростом наработки вероятность безотказной работы невосстанавливаемого объекта P(t) монотонно уменьшается от 1 при t = 0, асимптотически приближаясь к 0 при t →∞ , а вероятность отказа F(t) растет от 0 до 1 (рис. 4).
Вероятность безотказной работы объекта в интервале наработки (t, t + ∆t) есть условная вероятность того, что объект находится в работоспособном состоянии на этом интервале наработки, определяемая при условии, что объект сохранил работоспособность к моменту t начала этого интервала:
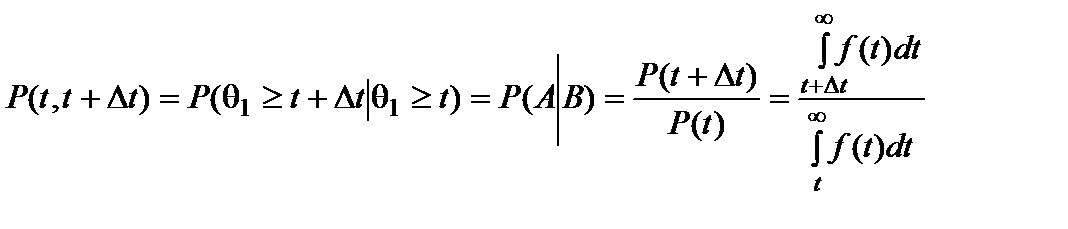 , (9)
, (9)
где P(B) – вероятность события B, состоящего в работоспособности объекта на интервале наработки (0, t) (рис. 5); P(A|B) – условная вероятность события A, состоящего в работоспособности объекта на интервале (t, t+∆t), определяемая при условии реализации события B; P(A∙B) – вероятность произведения (пересечения) случайных событий A и B ,т. е. вероятность работоспособности объекта на интервале (0, t+∆t).
Средняя наработка до отказа  – математическое ожидание наработки объекта до отказа. Иначе говоря,
– математическое ожидание наработки объекта до отказа. Иначе говоря,  есть «центр тяжести» распределения случайной величины θ1:
есть «центр тяжести» распределения случайной величины θ1:
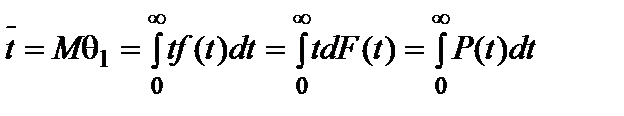 . (10)
. (10)
Таким образом, средняя наработка до отказа равна площади под кривой зависимости вероятности безотказной работы от наработки объекта.
| t |
| 0 t t+∆t A∙B |
| A |
| Рис. 5. Графическая интерпретация событий А и В во времени |
| B |
Гамма-процентная наработка до отказа tγ – наработка до отказа, которая обеспечивается для γ∙100% объектов рассматриваемого типа.
По определению,
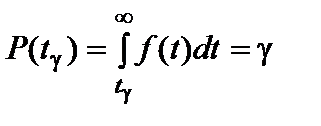 . (11)
. (11)
Вероятность отказа (интегральная функция распределения случайной величины θ1 – наработки объекта до отказа), отнесенная к моменту tγ, равна
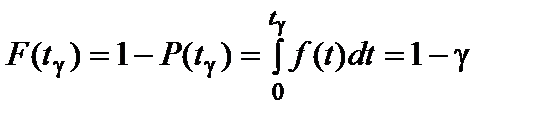 (12)
(12)
т.е. гамма-процентная наработка до отказа есть нижняя (1–γ)∙100%-ная квантиль распределения случайной величины θ1, а (1–γ)∙100% есть процент объектов, для которых отказы в течение наработки tγ допустимы.
Интенсивность отказов λ(t) – условная плотность вероятности возникновения отказа невосстанавливаемого объекта, определяемая для рассматриваемого момента наработки t при условии, что до этого момента отказ не возник.
По определению,
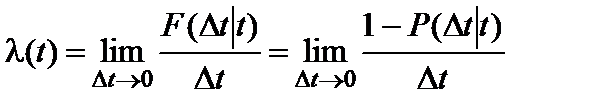 , (13)
, (13)
где F(∆t|t) – условная вероятность отказа объекта на интервале ∆t, определяемая при условии, что в момент t объект находился в работоспособном состоянии; P(∆t|t) – соответствующая вероятность безотказной работы.
Из (9) и (13) следует: 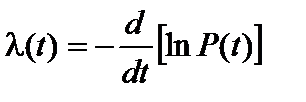 .
.
Интегрируя, получаем 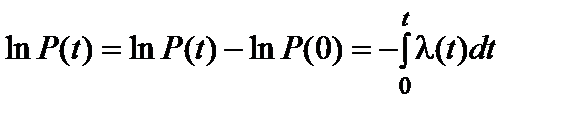 , откуда
, откуда
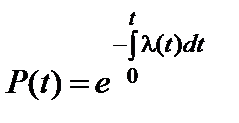 . (14)
. (14)
Формулу 14 называют основной формулой надежности.
На типичной кривой изменения интенсивности отказов невосстанавливаемого объекта (или параметра потока отказов восстанавливаемого объекта) с ростом наработки (рис. 6) выделяют три основных участка:
1. Начальный период эксплуатации (приработка). Повышенный уровень интенсивности отказов на этом участке объясняется скрытыми дефектами изготовления, которые, проявляясь в начальный период эксплуатации, приводят к отказам объекта.
2. Период нормальной эксплуатации. В течение этого периода, когда уровень накопленных повреждений, связанных с износом, еще не настолько высок, чтобы вызвать ухудшение выходных параметров объекта, интенсивность отказов (параметр потока отказов) обычно имеет стабильно низкое значение. Его уровень определяется особенностями объекта, исходным качеством, режимами и условиями эксплуатации. Обычно в течение этого периода эксплуатации наблюдается несколько характерных для данного объекта видов внезапных отказов, которые в совокупности определяют уровень интенсивности отказов (параметра потока отказов) на этом участке.
| λ(t) |
| Θt |
| x |
| 0 t uθ1 |
| Рис. 6. Изменение интенсивности отказов (параметра потока отказов) с наработкой |
3. Заключительный период эксплуатации (износ). В течение этого периода происходит прогрессирующее ухудшение выходных параметров объекта, обусловленное накоплением повреждений, вызванных износом и старением, что приводит к монотонному возрастанию интенсивности отказов (параметра потока отказов).
Параметр θt называют остаточной наработкой до отказа – это наработка объекта от момента контроля его технического состояния t до момента отказа θ1:
θt=θ1–t. (15)
Вероятность безотказной работы объекта, определяемая по его остаточной наработке, отсчитываемой с момента контроля технического состояния объекта t, равна
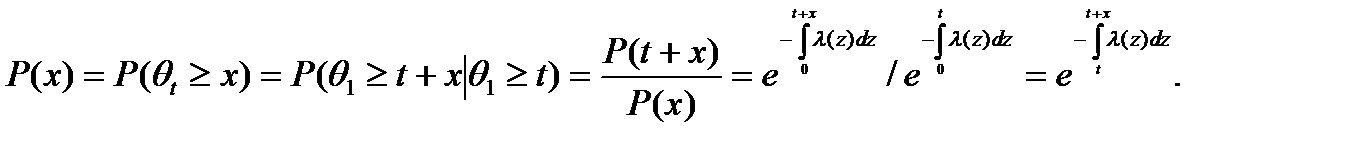 (16)
(16)
Следовательно, безотказность объекта, определяемая по его остаточной наработке, не зависит от изменения λ на интервале (0, t), т. е. до момента контроля технического состояния объекта.
Функция плотности распределения случайной величины θt – остаточной наработки до отказа
 , (17)
, (17)
где u = t + x.
Средняя остаточная наработка до отказа (математическое ожидание θt)
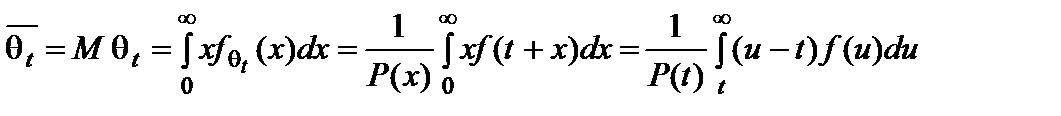 .(18)
.(18)
Установленная наработка до отказа tу – групповой показатель безотказности, соответствующий гамма-процентной наработке до отказа при уровне γ∙100% = 100%.
Данный показатель предполагает, что f(t) = 0 при t < tу. В вероятностном аспекте tу соответствует параметру сдвига. Например, в двухпараметрическом экспоненциальном законе распределения (рис.7) f(t)= λexp [–λ(t – c)] при t ≥ c ; f(t) = 0 при t < c.
Физический смысл показателя tу состоит в том, что на интервале (0, tу) отказы считаются невозможными событиями.
| Рис. 7. Плотность вероятности при установленной наработке до отказа |
| λ |
| f(t) |
| 0 tу=с t |
| Область высокой надежности |
В области высокой надежности (P(t)→1; t< tу), где вероятностные показатели надежности непредставительны, надежность характеризуют так называемым запасом надежности
Kн=Xmax/Xex, (19)
где Xmax – предельное значение выходного параметра X объекта, соответствующее наступлению отказа; Xex и Xexγ – предельные эксплуатационные значения выходного параметра по всей совокупности объектов и по γ∙100% объектов рассматриваемого типа (рис.8).
| 0 t tу tγ Mθ1 t |
| HL(t) |
| HH(t) |
| MX(t) |
| Hγ(t) |
| γ |
| 1-γ |
| f(t) |
| Xmax |
| Xex |
| Xexγ |
| Рис. 8. Схема исчерпания запаса надежности: HH(t), HL(t), Hγ(t) – верхняя, нижняя и γ-процентная границы области состояний объекта; MX(t) – кривая математического ожидания исчерпания запаса надежности объекта |
На интервале наработки (0, tу) запас надежности объекта Кн> 1; начиная с момента t=tу, запас надежности объекта считается исчерпанным (Кн =1); при t > tу отказы физически возможны. Скорость изменения запаса надежности объекта
 . (20)
. (20)
Дата добавления: 2015-03-19; просмотров: 1135;
