Термоактивируемые процессы

К термоактивируемым относятся процессы концентрационной диффузии, движения и взаимодействия дефектов, тепловых превращений (плавление, сублимация).

Термическая активация процесса заключается в том, что скорость или интенсивность процесса растут с увеличением энергии участвующих в процессе частиц. Температурная зависимость таких процессов характеризуется энергией активации. В статистической физике распределение частиц по энергиям описывается экспоненциальными зависимостями. Откуда зависимость скорости процесса от температуры имеет вид:

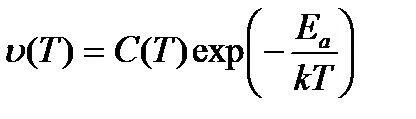. (1)

Здесь Е_а – энергия активации, С(Т) – константа процесса, в общем случае зависящая от температуры.

Экспоненциальными зависимостями от температуры хорошо описываются процессы старения, текучесть, ползучесть, усталость, трение, износ и пластическая деформация твёрдых материалов.

Макроскопические свойства материала, в конечном счёте, определяются состоянием и поведением дефектов на микроскопическом уровне. Дефекты кристаллической структуры разделяют на: точечные (вакансии, междоузельные атомы и др.), линейные (дислокации), поверхностные (границы зерен, дефекты упаковки и др.), объемные (пустоты, фазы, включения и др.). Для процессов возникновения отказов наибольшее значение имеют механизмы и кинетика образования, развития, перемещения и взаимодействия элементарных структурных дефектов – точечных дефектов и дислокаций и их взаимосвязь с макроскопическими свойствами материала.

Энергия, необходимая для образования точечного дефекта, определяется упругими искажениями кристаллической решетки и нарушениями периодической структуры кристалла. Эти процессы, как и процессы движения дислокаций, являются термоакивируемыми.

Энергия концентрационной диффузии в твёрдом теле – это энергия теплового движения атомов решетки. Многие структурные изменения в материалах являются следствием диффузионной подвижности атомов.

Скорость одномерной концентрационной диффузии в твердом теле описывается законом Фика:

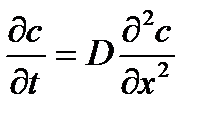, (2)

где: с – концентрация атомов, х – координата, D – коэффициент диффузии.