Момент силы относительно оси
Рассмотрим тело, к которому в точке А приложена сила  . Проведём через точку А плоскость xy, а затем ось z, перпендикулярную этой плоскости. Разложим силу
. Проведём через точку А плоскость xy, а затем ось z, перпендикулярную этой плоскости. Разложим силу  на составляющие: одну параллельно оси z и другую, лежащую в плоскости xy
на составляющие: одну параллельно оси z и другую, лежащую в плоскости xy  =
= 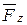 +
+ 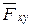 . Точку пересечения оси z с плоскостью xy обозначим буквой О. Сила Fz, параллельная оси z, не обладает вращательным эффектом; она только может переместить тело вдоль оси z (рис. 5.1).
. Точку пересечения оси z с плоскостью xy обозначим буквой О. Сила Fz, параллельная оси z, не обладает вращательным эффектом; она только может переместить тело вдоль оси z (рис. 5.1).
Вращательный эффект силы  может создавать составляющая
может создавать составляющая 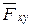 , следовательно, момент силы относительно оси равен моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью (рис. 5.1).
, следовательно, момент силы относительно оси равен моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью (рис. 5.1).
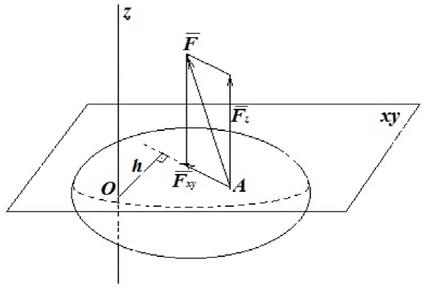
Рис. 5.1
Момент силы относительно оси равен нулю, если сила параллельна оси или когда сила пересекает ось, относительно которой определяется момент силы. Обобщая эти условия, можно заключить, что момент силы относительно оси равен нулю, когда сила и ось находятся в одной плоскости.
Для вычисления момент силы относительно оси z необходимо:
1) провести плоскость xy, перпендикулярную этой оси;
2) спроецировать на эту плоскость силу  и найти величину проекции
и найти величину проекции 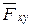 ;
;
3) опустить из точки О пересечения оси с плоскостью перпендикуляр на линию действия силы 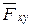 и найти длину перпендикуляра h;
и найти длину перпендикуляра h;
4) вычислить величину момента силы 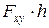 ;
;
5) определить знак момента силы. Момент силы  относительно оси z будет иметь знак «плюс», когда с положительного конца оси поворот, который стремится совершить сила
относительно оси z будет иметь знак «плюс», когда с положительного конца оси поворот, который стремится совершить сила 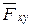 , будет виден происходящим против хода часовой стрелки, и знак «минус», когда по ходу часовой стрелки.
, будет виден происходящим против хода часовой стрелки, и знак «минус», когда по ходу часовой стрелки.
Таким образом, модуль момента силы  относительно оси z (рис. 5.1) равен:
относительно оси z (рис. 5.1) равен: 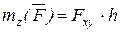 .
.
Дата добавления: 2015-03-17; просмотров: 1994;
