Порядок решения задач
1. Выделить одно тело системы, равновесие которого следует рассмотреть.
2. Приложить к выделенному телу все активные (заданные) силы. Если к телу приложена распределенная нагрузка, то ее необходимо заменить равнодействующей.
3. Освободить тело от связей, приложив соответствующие реакции. При этом необходимо убедиться, что данная задача является статически определимой.
4. Направить оси координат и выбрать моментные точки. Для каждого тела системы могут быть выбраны различные системы координат.
5. Составить уравнения равновесия произвольной плоской системы сил для выделенного тела.
Составляем уравнения равновесия по вышеизложенной схеме для каждого тела рассматриваемой системы. Все полученные уравнения равновесия решаем совместно, определяя неизвестные реакции связей.
Если в результате решения искомая реакция получается положительной, то это значит, что ее направление выбрано верно, если отрицательной, то истинное направление реакции противоположно выбранному (модуль же реакции определен верно).
После того, как задача решена, необходимо произвести проверку правильности решения. Для этого следует составить сумму моментов относительно точки, неиспользованной ранее при решении, при этом необходимо учитывать истинные направления реакций. Равенство нулю полученной суммы моментов подтвердит правильность решения задачи.
При решении подобных задач можно применять и другой прием. Можно рассмотреть условия равновесия для всей конструкции в целом (как для одного абсолютно твердого тела), а затем к этим трем уравнениям присоединить три уравнения равновесия, составленные только для одного из двух тел данной системы. Этот прием нередко предпочтительнее, так как в уравнения равновесия, составленные для всей системы в целом, входят только внешние силы и поэтому эти уравнения оказываются, обычно, проще.
Пример 1. Определить внешние (опорные) и внутренние связи рамы, изображенной на рис. 3.4, при следующих исходных данных: q=2кН/м, P=4кН.
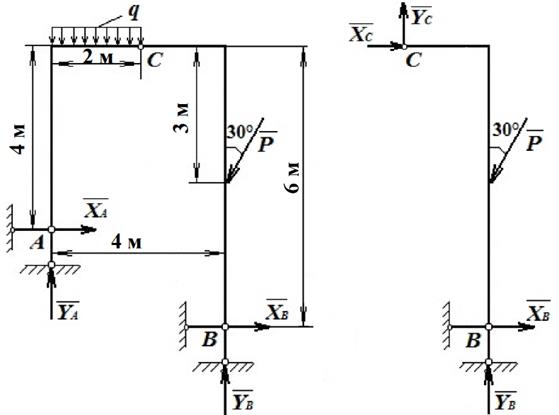
Рис. 3.4
Решение.
Составим уравнения равновесия для всей конструкции:
| ∑ Fkx = 0; XA – P·sin30° + XB = 0; | (1) |
| ∑ Fky = 0 ; YA – 2·q - P·cos30° + YB = 0; | (2) |
| ∑ mA(Fk) = 0; 2·XВ + 4·YВ - 4·P·cos30° + 1·P·sin30° - q·2·1 = 0. | (3) |
Уравнения равновесия для правой части рамы:
| ∑ Fkx = 0; XC –P·sin30° + XB = 0; | (4) |
| ∑ Fky = 0; YC – P·cos30° + YB = 0; | (5) |
| ∑ mС(Fk) = 0; 6·XB + 2·YB – 2·P·cos30° - 3·P·sin30° = 0. | (6) |
Решая совместно уравнения (3) и (6), получим:
XВ = 1кН; YB = 3,464кН.
Подставляя найденные значения XВ и YB в уравнения (1) и (2) определим реакции опоры А:
XА = 1кН; YА = 4кН.
Из уравнений (4) и (5) определим реакции внутренних связей:
XС = 1кН; YС = 0кН.
Сделаем проверку, составив уравнение моментов для всей конструкции относительно точки В:
∑ mВ(Fk) = 0; 3·P·sin30° + q·2·3 - 2·XА - 4·YА = 0.
Подставляя численные значения, получаем:
4·0,5·3 + 2·2·3 – 1·2 – 4·4 = 0; 6 + 12 – 2 – 16 = 0; 18 – 18 = 0.
Ответ:
| XC = ±1кН, | XA = 1кН, | XВ = 1кН, |
| YC = 0кН, | YA =4кН, | YB =3,464кН. |
Поскольку силы XC и YC – внутренние, то знак силы определяется в зависимости от того, для какой части конструкции рассматривается равновесие.
В том случае, когда части конструкции опираются друг на друга, или когда одна из опор является гладкой поверхностью, целесообразно сразу расчленять систему на отдельные тела и составлять уравнения равновесия для каждого тела в отдельности (см. рис.3.5). При этом реакции внутренних связей будут попарно равны по модулю и противоположны по направлению.
Для расчета составной конструкции (рис. 3.5) следует сразу расчленить конструкцию и рассмотреть равновесие балки DЕ. Уравнение равновесия балки DЕ будет содержать только три неизвестные реакции ХD, YD, NE. Определив внутреннюю реакцию связи NE, нетрудно найти внешние реакции связи балки АВ: XА, YА, NВ.
Пример 2. Однородная балка АВ весом Р2= 2 кН и длиной 6 м удерживается в горизонтальной плоскости с помощью неподвижной шарнирной опоры и гладкой опоры.
На балку АВ свободно опирается однородная балка DЕ весом Р1=1,5 кН и длиной 6 м. К балке DE в точке C приложена сила F=1 кН на расстоянии DC = 4 м.
Определить опорные реакции и силу взаимодействия балок AB и DE (рис. 3.5).
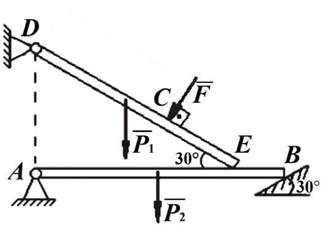
Рис. 3.5
Решение. Заданную конструкцию расчленим на систему тел (рис.3.6) и рассмотрим равновесие сначала балки DЕ, а затем балки АВ.
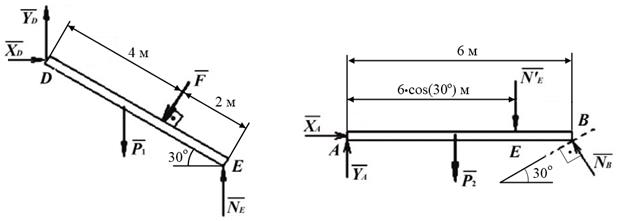
Рис. 3.6
Уравнения равновесия балки DЕ:
∑ Fkx = 0; XD –F·cos60° = 0;
∑ Fky = 0; YD – F·sin60° - P1 + NE = 0;
∑ mD(  ) = 0; NE·DE·cos30°- F·DC - P1·(DE/2)·cos30° = 0.
Уравнения равновесия балки АВ:
∑ Fkx = 0; XA –NB·cos60° = 0;
∑ Fky = 0; YA – P2 - NE´ + NB·cos30° = 0;
∑ mA( ) = 0; NE·DE·cos30°- F·DC - P1·(DE/2)·cos30° = 0.
Уравнения равновесия балки АВ:
∑ Fkx = 0; XA –NB·cos60° = 0;
∑ Fky = 0; YA – P2 - NE´ + NB·cos30° = 0;
∑ mA( 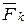 ) = 0; NB·cos30°·AB - NE´·АE - P2·(AB/2)= 0. ) = 0; NB·cos30°·AB - NE´·АE - P2·(AB/2)= 0.
| (1) (2) (3) (4) (5) (6) |
Из уравнения (1): XD = F·cos60° = 1·0,5 = 0,5кН.
Из уравнения (3): NE = (F·4 + P1·DE/2·cos30°)/(DE·cos30°) = 1,52кН.
Из уравнения (6): NB = (NE´·АE + P2·AB/2)/(AB·cos30°) = 2,67кН.
Ответ: XD = 0,5кН, YD = 0,85кН, XA = 1,35кН, YA = 1,21кН, NB=2,67 кН.
Проверка: Составим уравнение моментов относительно точки D для всей конструкции:
∑ mD( 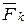 ) = 0;
) = 0;
-P1·DE/2·cos30°-F·CD-P2·AB/2+AB·NB·cos30°-DA·NB·cos60°+ XA·DA=0;
DA= DE·cos60°=6·cos60°=3м.
-1,5·6/2·cos30°-1·4-2·6/2+6·2,67·cos30°-3··2,67·cos60°+1,35·3=0; 0≈0.
Проверка сошлась.
Дата добавления: 2015-03-17; просмотров: 3677;
