ПРОСТЕЙШИЕ ВЫЧИСЛЕНИЯ В MATLAB

В табл. 10.1 приведены модели изменения параметров ряда изделий машиностроения, построенные на основе качественного описания природы процессов, приводящих к отказам.

Модели изменения параметров Таблица 10.1

Параметр, характеризующий изменение прочности	Устройство	Качественное описание физики процесса	Математическая модель
Размер уплотнения	Силовой цилиндр, клапан	Изменение состояния и свойств материала под действием повторных переменных напряжений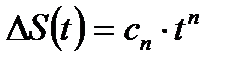
Величина зазора	Плунжерная пара насоса, торцевое уплотнение	Механический абразивный износ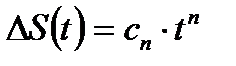
Конусность	Кран, вентиль	Контактная усталость рабочих поверхностей деталей с образованием микротрещин и других дефектов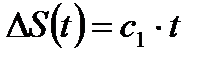
Режущий угол инструмента	Резец, фреза	Изменение состояния материала режущей кромки под воздействием механического выламывания частиц в результате абразивного износа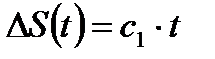
Глубина профиля	Автопокрышка	Изменение состояния материала под действием многократных нагрузок на поверхностный слой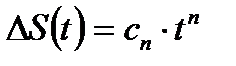
Изменение диаметра валов	Валы	Окисление поверхностных слоев металла и последующее разрушение окислов при действии незначительных повторных возвратно-поступательных перемещений несопрягаемых деталей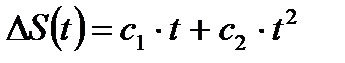
Величина потока жидкости	Распределительное устройство в гидросистеме	Изменение состояния и свойств материала деталей системы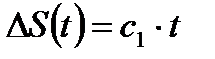
Величина утечки жидкости или газа	Гидро- и пневмоцилиндры	Изменение состояния и свойств материала под действием повторных переменных напряжений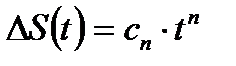
Перепад давления	Насос, гидромотор, входящий в систему гидропривода	Изменение состояния и свойств материала под действием повторных переменных напряжений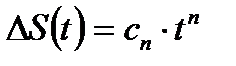
Скорость проходки, величина подачи	Буровой инструмент	Основной механизм разрушения – механический износ, характеризующийся выкрашиванием режущей кромки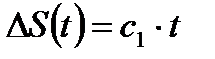
Значение нормального и касательного напряжений	Рама автомобиля	Изменение состояния и свойств материала, связанное с накоплением усталостных повреждений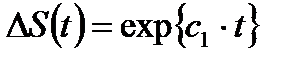
Давление страгивания	Гидроцилиндр	Изменение состояния и свойств материала под действием повторных переменных напряжений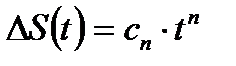
Потеря мощности в системе	Двигатель внутреннего сгорания	Изменение состояния и свойств поршневых колец, характеризуется отрывом частиц металла под действием горячих газов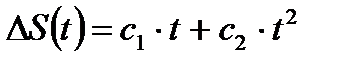
Увеличение температуры в системе	Система с уплотнительными кольцами	Происходит схватывание отдельных атомов цветного металла и перенос их на стальную поверхность, что приводит к появлению на рабочих поверхностях рисок изадиров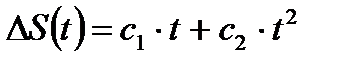
Величина усилия прижатия	Пресс	Изменение состояния и свойств материала под действием повторных переменных напряжений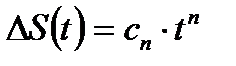

Хорошей аппроксимацией деградационных процессов старения являются регрессивные модели полиномиального вида.

Для металлургических машин характерен периодический режим работы: определенный период работы чередуется с периодом простоя, в течение которого можно осуществлять контроль текущего состояния и при необходимости ремонтно – профилактическое обслуживание (полеты самолетов, сменная работа станков и пр.)

Для таких изделий важно не только определить состояние в момент контроля, но и осуществить контроль динамики этого состояния на один шаг вперед, где величина шага зависит от периода работы (время полета, смена).

Специфика функционирования изделий данного класса определяет требования, предъявляемые к методу идентификации деградационных процессов старения. Действительно, модели старения в основном являются эмпирическими, хорошо аппроксимирующими реальные процессы лишь в ограниченном отрезке времени. Для аппроксимации могут быть применены полиномиальные модели невысокого порядка, в том числе наиболее простые – нулевого и первого порядков, поскольку шаг прогнозирования мал по сравнению со временем функционирования изделия.

Алгоритм идентификации так же, как и функционирование изделий, должен иметь пошаговый характер с последовательной корректировкой оценок состояния на каждом шагу.

Таким образом, наиболее рациональным методом идентификации деградационных процессов старения является рекуррентная форма регрессивного анализа – метода наименьших квадратов.

Особенность всех рекуррентных алгоритмов – сильная зависимость их сходимости от выбора начальных условий. Учитывая, однако, принятую аппроксимацию модели старения, могут быть даны некоторые рекомендации по необходимому числу экспериментальных точек.

Так, если ограничиться постоянным членом y = c₀, то оценка наименьших квадратов этого постоянного члена имеет вид

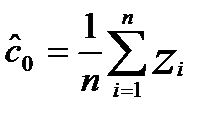, (10.1)

при этом дисперсия оценки по сравнению с дисперсией одного измерения уменьшается в n раз:

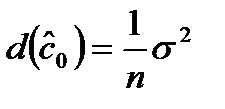, (10.2)

При использовании линейной аппроксимации y = c₁t оценка наименьших квадратов параметра c₁ имеет вид

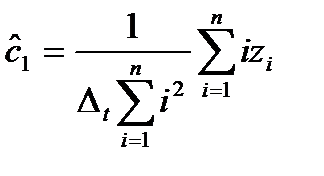, (10.3)

Сумма 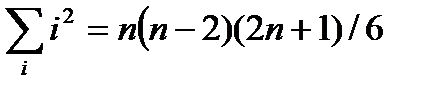и при больших значениях n 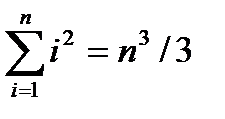, т.е. дисперсия оценки 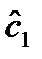пропорциональна 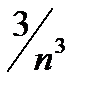и уже начиная с n=2 меньше, чем дисперсия оценки .

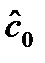Аналогично при использовании аппроксимации y = с_k t^k оценка наименьших квадратов имеет вид [7]:

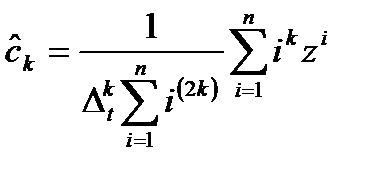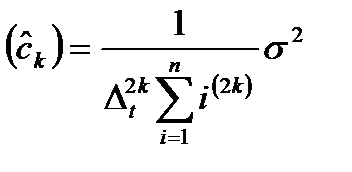, d . (10.4)

Таким образом, число экспериментальных точек может быть выбрано из условия обеспечения удовлетворительной точности при наиболее простой пошаговой аппроксимации нулевого порядка. Величина интервала Δt определяется технико-экономическими показателями контрольно-измерительного комплекса.

ПРОСТЕЙШИЕ ВЫЧИСЛЕНИЯ В MATLAB

Система компьютерной математики MATLAB (Matrix Lавoratory) переводится с английского как «Матричная лаборатория». Она является одним из эффективнейших средств выполнения научных и инженерных расчетов, их визуализации, обработки результатов эксперимента, анализа и моделирования. Для формулировки и решения задач в среде MATLAB используются понятные математические выражения, близкие к традиционным формулам, связывающие векторные или матричные объекты. Система включает ядро, использующее базовые вычислительные (встроенные) функции, и набор общематематических, графических и проблемно - ориентированных пакетов (Toolboxes), позволяющих изучать и применять современную вычислительную технологию в таких областях, как обработка сигналов и изображений, моделирование, системы управления, системы связи, нейронные сети и многие другие.

Данное учебное пособие посвящено описанию рабочей среды MATLAB6.x и выполнению элементарных операций с числами и массивами в командном режиме (режиме калькулятора). В нем рассматриваются особенности задания в MATLAB действительных и комплексных чисел, форматы их представления, правила использования переменных, а также способы задания векторов и матриц. Здесь также рассмотрены встроенные математические функции и способы сохранения переменных для их использования в последующих сеансах работы в MATLAB. Обсуждаются некоторые распространенные затруднения, с которыми можно столкнуться. Рекомендуется читать это пособие и параллельно работать с командами, экспериментировать с вариантами примеров.

Предполагается, что пользователь знаком с каким-либо языком программирования, например Pascalили Basic, с приемами, общими для Windows - приложений и математическими постановками рассматриваемых задач.

Для реализации всех рассматриваемых примеров на используемом компьютере должны быть установлены следующие компоненты системы: ядро MATLAB, пакет Symbolic Math Toolbox.